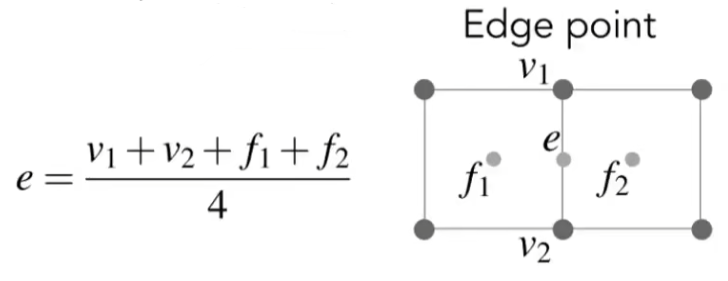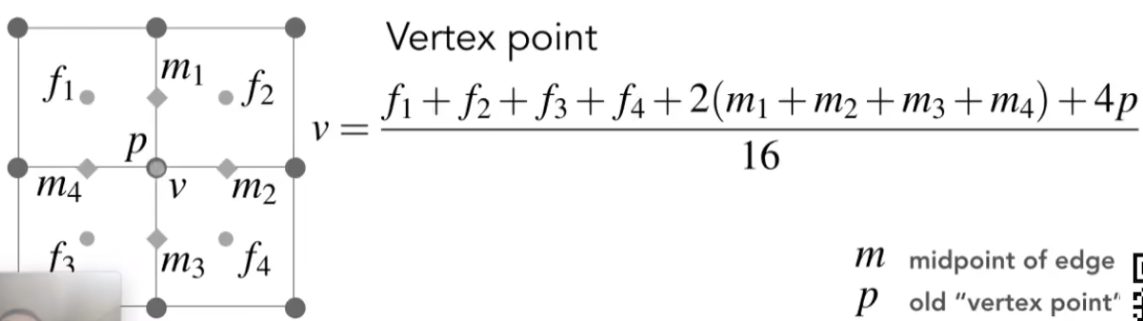课程链接:https://www.bilibili.com/video/BV1X7411F744
作业仓库:https://github.com/Tanyuu/GAMES101-Homework1-8
向量叉乘不同于点乘(a ⃗ ⋅ b ⃗ = a ⃗ T b ⃗ = [ x a y a z a ] [ x a y a z a ] \vec{a}\cdot\vec{b}=\vec{a}^T\vec{b}=\begin{bmatrix}x_a&y_a&z_a\end{bmatrix}\begin{bmatrix}x_a\\y_a\\z_a\end{bmatrix} a ⋅ b = a T b = [ x a y a z a ] ⎣ ⎡ x a y a z a ⎦ ⎤
a ⃗ × b ⃗ = [ a ] × b = [ 0 − z a y a z a 0 − x a − y a x a 0 ] [ x a y a z a ] \vec a\times\vec b=[a]_\times b=
\begin{bmatrix}
0&-z_a&y_a\\
z_a&0&-x_a\\
-y_a&x_a&0
\end{bmatrix}
\begin{bmatrix}x_a\\y_a\\z_a\end{bmatrix}
a × b = [ a ] × b = ⎣ ⎡ 0 z a − y a − z a 0 x a y a − x a 0 ⎦ ⎤ ⎣ ⎡ x a y a z a ⎦ ⎤
变换包含若干细分,如Viewing(视角变换)和Modeling(模型变换);
仿射变换形式如下:
[ x ′ y ′ ] = [ a b c d ] [ x y ] + [ e f ] \begin{bmatrix}
x'\\y'
\end{bmatrix}
=
\begin{bmatrix}
a&b\\c&d
\end{bmatrix}
\begin{bmatrix}
x\\y
\end{bmatrix}
+
\begin{bmatrix}
e\\f
\end{bmatrix}
[ x ′ y ′ ] = [ a c b d ] [ x y ] + [ e f ]
比如平移变换(Translation Transformation)(T ( t x , t y ) T{(t_x,t_y)} T ( t x , t y )
[ x ′ y ′ ] = [ 1 0 0 1 ] [ x y ] + [ t x t y ] \begin{bmatrix}
x'\\y'
\end{bmatrix}
=
\begin{bmatrix}
1&0\\0&1
\end{bmatrix}
\begin{bmatrix}
x\\y
\end{bmatrix}
+
\begin{bmatrix}
t_x\\t_y
\end{bmatrix}
[ x ′ y ′ ] = [ 1 0 0 1 ] [ x y ] + [ t x t y ]
对于这种形式,仿射变换并不能像其他变换一样用单纯的用矩阵乘法进行表示。为了方便表示,我们引入了齐次坐标(我更愿意翻译为“同坐标”),形式如下:
[ x y ω ] \begin{bmatrix}
x\\y\\\omega
\end{bmatrix}
⎣ ⎡ x y ω ⎦ ⎤
若 ω \omega ω [ x y ω ] \begin{bmatrix}
x\\y\\\omega
\end{bmatrix} ⎣ ⎡ x y ω ⎦ ⎤ [ x ω y ω 1 ] \begin{bmatrix}\frac x \omega\\\frac y\omega\\1\end{bmatrix} ⎣ ⎡ ω x ω y 1 ⎦ ⎤ ( x ω , y ω ) (\frac x\omega,\frac y\omega) ( ω x , ω y )
。
齐次坐标还有一些神奇的性质,它使得点与向量间的运算封闭:q
向量+向量=向量
点+向量=点
向量-向量=向量
点-向量=点+(-向量)=点
向量-点=点
点+点=中点
齐次坐标表示下,平移变换(T ( t x , t y ) T{(t_x,t_y)} T ( t x , t y )
[ x ′ y ′ ω ′ ] = [ 1 0 t x 0 1 t y 0 0 1 ] [ x y ω ] = [ x + ω t x y + ω t y ω ] \begin{bmatrix}
x'\\y'\\\omega'
\end{bmatrix}
=
\begin{bmatrix}
1&0&t_x\\
0&1&t_y\\
0&0&1
\end{bmatrix}
\begin{bmatrix}
x\\y\\\omega
\end{bmatrix}
=
\begin{bmatrix}
x+\omega t_x\\y+\omega t_y\\\omega
\end{bmatrix}
⎣ ⎡ x ′ y ′ ω ′ ⎦ ⎤ = ⎣ ⎡ 1 0 0 0 1 0 t x t y 1 ⎦ ⎤ ⎣ ⎡ x y ω ⎦ ⎤ = ⎣ ⎡ x + ω t x y + ω t y ω ⎦ ⎤
解决了前述问题。
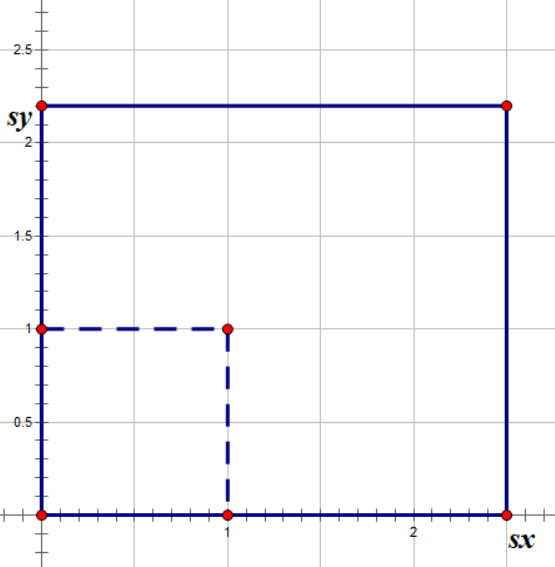
横轴缩放 s x s_x s x s y s_y s y S ( s x , s y ) S{(s_x,s_y)} S ( s x , s y )
[ x ′ y ′ ω ′ ] = [ s x 0 0 0 s y 0 0 0 1 ] [ x y ω ] = [ x s x y s y ω ] \begin{bmatrix}
x'\\y'\\\omega'
\end{bmatrix}
=
\begin{bmatrix}
s_x&0&0\\
0&s_y&0\\
0&0&1
\end{bmatrix}
\begin{bmatrix}
x\\y\\\omega
\end{bmatrix}=\begin{bmatrix}
xs_x\\ys_y\\\omega
\end{bmatrix}
⎣ ⎡ x ′ y ′ ω ′ ⎦ ⎤ = ⎣ ⎡ s x 0 0 0 s y 0 0 0 1 ⎦ ⎤ ⎣ ⎡ x y ω ⎦ ⎤ = ⎣ ⎡ x s x y s y ω ⎦ ⎤
若 s ∗ < 0 s_*<0 s ∗ < 0
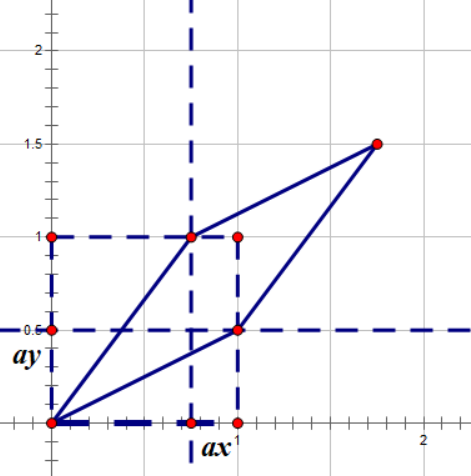
符合 x ′ = x + a x y , y ′ = y + a y x x'=x+a_xy,y'=y+a_yx x ′ = x + a x y , y ′ = y + a y x
[ x ′ y ′ ω ′ ] = [ 1 a x 0 a y 1 0 0 0 1 ] [ x y ω ] = [ x + a x y y + a y x ω ] \begin{bmatrix}
x'\\y'\\\omega'
\end{bmatrix}
=
\begin{bmatrix}
1&a_x&0\\
a_y&1&0\\
0&0&1
\end{bmatrix}
\begin{bmatrix}
x\\y\\\omega
\end{bmatrix}=\begin{bmatrix}
x+a_xy\\y+a_yx\\\omega
\end{bmatrix}
⎣ ⎡ x ′ y ′ ω ′ ⎦ ⎤ = ⎣ ⎡ 1 a y 0 a x 1 0 0 0 1 ⎦ ⎤ ⎣ ⎡ x y ω ⎦ ⎤ = ⎣ ⎡ x + a x y y + a y x ω ⎦ ⎤
旋转变换默认绕 ( 0 , 0 ) (0,0) ( 0 , 0 ) x + x^+ x +
旋转 θ \theta θ R θ R_\theta R θ
[ x ′ y ′ ω ′ ] = [ cos θ − sin θ 0 sin θ cos θ 0 0 0 1 ] [ x y ω ] \begin{bmatrix}
x'\\y'\\\omega'
\end{bmatrix}
=
\begin{bmatrix}
\cos\theta&-\sin\theta&0\\
\sin\theta&\cos\theta&0\\
0&0&1
\end{bmatrix}
\begin{bmatrix}
x\\y\\\omega
\end{bmatrix}
⎣ ⎡ x ′ y ′ ω ′ ⎦ ⎤ = ⎣ ⎡ cos θ sin θ 0 − sin θ cos θ 0 0 0 1 ⎦ ⎤ ⎣ ⎡ x y ω ⎦ ⎤
结合下述的逆变换,我们可以发现:
R ( − θ ) = [ cos θ sin θ − sin θ cos θ ] = R ( θ ) T R ( − θ ) = R ( θ ) − 1 R{(-\theta)}=
\begin{bmatrix}
\cos\theta&\sin\theta\\
-\sin\theta&\cos\theta
\end{bmatrix}
=R{(\theta)}^T\\
R{(-\theta)}=R{(\theta)}^{-1}
R ( − θ ) = [ cos θ − sin θ sin θ cos θ ] = R ( θ ) T R ( − θ ) = R ( θ ) − 1
若 A ′ A' A ′ A A A M M M A ′ = M A A'=MA A ′ = M A A A A A ′ A' A ′ M − 1 M^{-1} M − 1 A = M − 1 A ′ A=M^{-1}A' A = M − 1 A ′
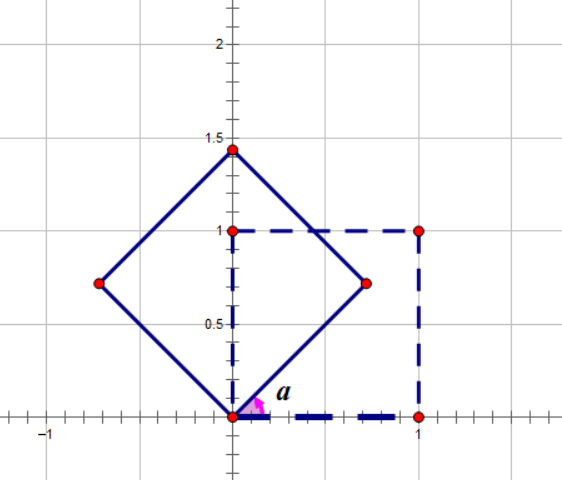
若先进行 R ( 45 ° ) R{(45\degree)} R ( 4 5 ° ) T ( 1 , 0 ) T{(1,0)} T ( 1 , 0 )
A → R ( 45 ° ) R ( 45 ° ) A → T ( 1 , 0 ) T ( 1 , 0 ) R ( 45 ° ) A A\xrightarrow{R{(45\degree)}}R{(45\degree)}A\xrightarrow{T{(1,0)}}T{(1,0)}R{(45\degree)}A
A R ( 4 5 ° ) R ( 4 5 ° ) A T ( 1 , 0 ) T ( 1 , 0 ) R ( 4 5 ° ) A
最终的式子 T ( 1 , 0 ) R ( 45 ° ) A T{(1,0)}R{(45\degree)}A T ( 1 , 0 ) R ( 4 5 ° ) A T ( 1 , 0 ) R ( 45 ° ) T{(1,0)}R{(45\degree)} T ( 1 , 0 ) R ( 4 5 ° ) A A A
一般地,如果向量 A A A M 1 , M 2 , … , M n M_1,M_2,\dots,M_n M 1 , M 2 , … , M n
M n ( … M 2 ( M 1 ( A ) ) ) = ( M n … M 2 M 1 ) A M_n(\dots M_2(M_1(A)))=(M_n\dots M_2M_1)A
M n ( … M 2 ( M 1 ( A ) ) ) = ( M n … M 2 M 1 ) A
考虑平移矩阵(T ( t x , t y ) T_{(t_x,t_y)} T ( t x , t y )
[ x ′ y ′ ω ′ ] = [ 1 0 t x 0 1 t y 0 0 1 ] [ x y ω ] \begin{bmatrix}
x'\\y'\\\omega'
\end{bmatrix}
=
\begin{bmatrix}
1&0&t_x\\
0&1&t_y\\
0&0&1
\end{bmatrix}
\begin{bmatrix}
x\\y\\\omega
\end{bmatrix}
⎣ ⎡ x ′ y ′ ω ′ ⎦ ⎤ = ⎣ ⎡ 1 0 0 0 1 0 t x t y 1 ⎦ ⎤ ⎣ ⎡ x y ω ⎦ ⎤
其左上的 ( 2 , 2 ) (2,2) ( 2 , 2 ) ( 2 , 2 ) (2,2) ( 2 , 2 )
上述的旋转变换是绕原点进行的,如果要绕 c c c − c -c − c c c c α \alpha α
A → T ( − c ) T ( − c ) A → R ( α ) R ( α ) T ( c ) A → T ( − c ) T ( c ) R ( α ) T ( − c ) A A\xrightarrow{T{(-c)}}T{(-c)}A\xrightarrow{R{(\alpha)}}R{(\alpha)}T{(c)}A\xrightarrow{T{(-c)}}T{(c)}R{(\alpha)}T{(-c)}A
A T ( − c ) T ( − c ) A R ( α ) R ( α ) T ( c ) A T ( − c ) T ( c ) R ( α ) T ( − c ) A
T ( t x , t y , t z ) = [ 1 0 0 t x 0 1 0 t y 0 0 1 t z 0 0 0 1 ] T{(t_x,t_y,t_z)}=
\begin{bmatrix}
1&0&0&t_x\\
0&1&0&t_y\\
0&0&1&t_z\\
0&0&0&1
\end{bmatrix}
T ( t x , t y , t z ) = ⎣ ⎢ ⎢ ⎡ 1 0 0 0 0 1 0 0 0 0 1 0 t x t y t z 1 ⎦ ⎥ ⎥ ⎤
S ( s x , s y , s z ) = [ s x 0 0 0 0 s y 0 0 0 0 s z 0 0 0 0 1 ] S{(s_x,s_y,s_z)}=
\begin{bmatrix}
s_x&0&0&0\\
0&s_y&0&0\\
0&0&s_z&0\\
0&0&0&1
\end{bmatrix}
S ( s x , s y , s z ) = ⎣ ⎢ ⎢ ⎡ s x 0 0 0 0 s y 0 0 0 0 s z 0 0 0 0 1 ⎦ ⎥ ⎥ ⎤
R x ( α ) = [ 1 0 0 0 0 cos α − sin α 0 0 sin α cos α 0 0 0 0 1 ] R y ( α ) = [ cos α 0 sin α 0 0 1 0 0 − sin α 0 cos α 0 0 0 0 1 ] R z ( α ) = [ cos α − sin α 0 0 sin α cos α 0 0 0 0 1 0 0 0 0 1 ] R_x(\alpha)=
\begin{bmatrix}
1&0&0&0\\
0&\cos\alpha&-\sin\alpha&0\\
0&\sin\alpha&\cos\alpha&0\\
0&0&0&1
\end{bmatrix}\\
R_y(\alpha)=
\begin{bmatrix}
\cos\alpha&0&\sin\alpha&0\\
0&1&0&0\\
-\sin\alpha&0&\cos\alpha&0\\
0&0&0&1
\end{bmatrix}\\
R_z(\alpha)=
\begin{bmatrix}
\cos\alpha&-\sin\alpha&0&0\\
\sin\alpha&\cos\alpha&0&0\\
0&0&1&0\\
0&0&0&1
\end{bmatrix}\\
R x ( α ) = ⎣ ⎢ ⎢ ⎡ 1 0 0 0 0 cos α sin α 0 0 − sin α cos α 0 0 0 0 1 ⎦ ⎥ ⎥ ⎤ R y ( α ) = ⎣ ⎢ ⎢ ⎡ cos α 0 − sin α 0 0 1 0 0 sin α 0 cos α 0 0 0 0 1 ⎦ ⎥ ⎥ ⎤ R z ( α ) = ⎣ ⎢ ⎢ ⎡ cos α sin α 0 0 − sin α cos α 0 0 0 0 1 0 0 0 0 1 ⎦ ⎥ ⎥ ⎤
由于循环对称性,x + = y + × z + , z + = x + × y + x^+=y^+\times z^+,z^+=x^+\times y^+ x + = y + × z + , z + = x + × y + y + = z + × x + y^+=z^+\times x^+ y + = z + × x + R y ( α ) R_y(\alpha) R y ( α ) x + , z + x^+,z^+ x + , z + y + y^+ y +
将任意旋转分解为 x , y , z x,y,z x , y , z α , β , γ \alpha,\beta,\gamma α , β , γ
R x y z ( α , β , γ ) = R x ( α ) R y ( β ) R z ( γ ) R_{xyz}(\alpha,\beta,\gamma)=R_x(\alpha)R_y(\beta)R_z(\gamma)
R x y z ( α , β , γ ) = R x ( α ) R y ( β ) R z ( γ )
绕旋转轴 n ⃗ \vec n n n ⃗ \vec n n ⨀ \bigodot ⨀ α \alpha α
R ( n ⃗ , α ) = [ 0 cos ( α ) I 0 0 0 0 0 1 ] + ( 1 − cos ( α ) ) [ n ⃗ 0 ] [ n ⃗ 0 ] T + sin ( α ) [ 0 − n z n y 0 n z 0 − n x 0 − n y n x 0 0 0 0 0 0 ] R(\vec n,\alpha)=
\begin{bmatrix}
&&&0\\
&\cos(\alpha)I&&0\\
&&&0\\
0&0&0&1
\end{bmatrix}
+
(1-\cos(\alpha))
\begin{bmatrix}
\vec n\\
0
\end{bmatrix}
\begin{bmatrix}
\vec n\\
0
\end{bmatrix}
^T+\sin(\alpha)
\begin{bmatrix}
0&-n_z&n_y&0\\
n_z&0&-n_x&0\\
-n_y&n_x&0&0\\
0&0&0&0
\end{bmatrix}
R ( n , α ) = ⎣ ⎢ ⎢ ⎡ 0 cos ( α ) I 0 0 0 0 0 1 ⎦ ⎥ ⎥ ⎤ + ( 1 − cos ( α ) ) [ n 0 ] [ n 0 ] T + sin ( α ) ⎣ ⎢ ⎢ ⎡ 0 n z − n y 0 − n z 0 n x 0 n y − n x 0 0 0 0 0 0 ⎦ ⎥ ⎥ ⎤
其中 I I I 3 × 3 3\times 3 3 × 3 sin ( α ) [ n ⃗ ] × \sin(\alpha)[\vec n]_\times sin ( α ) [ n ] ×
如果旋转轴不经过原点,可以再通过两次平移完成旋转过程;
将三维的点集由世界坐标变换为相机坐标;
相机有如下几种属性:位置(Position)e ⃗ \vec e e g ^ \hat g g ^ t ^ \hat t t ^
我们将原坐标系变换为相机坐标系,并符合如下规则:相机在原点、向上方向为 y + y^+ y + z − z^- z − x + is g × t , y + is t , z + is − g x^+\text{ is }g\times t,y^+\text{ is }t,z^+\text{ is }-g x + is g × t , y + is t , z + is − g
假设变换矩阵为 M v i e w M_{view} M v i e w M v i e w = R v i e w T v i e w M_{view}=R_{view}T_{view} M v i e w = R v i e w T v i e w T v i e w = T ( − e ⃗ ) T_{view}=T_{(-\vec e)} T v i e w = T ( − e )
考虑 R v i e w − 1 R_{view}^{-1} R v i e w − 1 参考
R v i e w − 1 = [ x g ^ × t ^ x t ^ x − g ^ 0 y g ^ × t ^ y t ^ y − g ^ 0 z g ^ × t ^ z t ^ z − g ^ 0 0 0 0 1 ] R_{view}^{-1}=
\begin{bmatrix}
x_{\hat g\times\hat t}&x_{\hat t}&x_{-\hat g}&0\\
y_{\hat g\times\hat t}&y_{\hat t}&y_{-\hat g}&0\\
z_{\hat g\times\hat t}&z_{\hat t}&z_{-\hat g}&0\\
0&0&0&1
\end{bmatrix}
R v i e w − 1 = ⎣ ⎢ ⎢ ⎡ x g ^ × t ^ y g ^ × t ^ z g ^ × t ^ 0 x t ^ y t ^ z t ^ 0 x − g ^ y − g ^ z − g ^ 0 0 0 0 1 ⎦ ⎥ ⎥ ⎤
得:
R v i e w = [ x g ^ × t ^ y g ^ × t ^ z g ^ × t ^ 0 x t ^ y t ^ z t ^ 0 x − g ^ y − g ^ z − g ^ 0 0 0 0 1 ] R_{view}=
\begin{bmatrix}
x_{\hat g\times\hat t}&y_{\hat g\times\hat t}&z_{\hat g\times\hat t}&0\\
x_{\hat t}&y_{\hat t}&z_{\hat t}&0\\
x_{-\hat g}&y_{-\hat g}&z_{-\hat g}&0\\
0&0&0&1
\end{bmatrix}
R v i e w = ⎣ ⎢ ⎢ ⎡ x g ^ × t ^ x t ^ x − g ^ 0 y g ^ × t ^ y t ^ y − g ^ 0 z g ^ × t ^ z t ^ z − g ^ 0 0 0 0 1 ⎦ ⎥ ⎥ ⎤
简略来说,进行相机变换之后,将 z z z x , y x,y x , y ( − ∞ , + ∞ ) 2 (-\infty,+\infty)^2 ( − ∞ , + ∞ ) 2 [ − 1 , 1 ] 2 [-1,1]^2 [ − 1 , 1 ] 2
但是正式来说,首先定义相机变换后空间中的一个立方体(视景体),具有在 x x x [ l , r ] [l,r] [ l , r ] y y y [ b , t ] [b,t] [ b , t ] z z z [ f , n ] [f,n] [ f , n ] [ − 1 , 1 ] 3 [-1,1]^3 [ − 1 , 1 ] 3
M o r t h o = [ 2 r − l 0 0 0 0 2 t − b 0 0 0 0 2 n − f 0 0 0 0 1 ] [ 1 0 0 − r + l 2 0 1 0 − t + b 2 0 0 1 − n + f 2 0 0 0 1 ] M_{ortho}=
\begin{bmatrix}
\frac 2 {r-l}&0&0&0\\
0&\frac 2 {t-b}&0&0\\
0&0&\frac 2 {n-f}&0\\
0&0&0&1
\end{bmatrix}
\begin{bmatrix}
1&0&0&-\frac {r+l}2\\
0&1&0&-\frac {t+b}2\\
0&0&1&-\frac {n+f}2\\
0&0&0&1
\end{bmatrix}
M o r t h o = ⎣ ⎢ ⎢ ⎡ r − l 2 0 0 0 0 t − b 2 0 0 0 0 n − f 2 0 0 0 0 1 ⎦ ⎥ ⎥ ⎤ ⎣ ⎢ ⎢ ⎡ 1 0 0 0 0 1 0 0 0 0 1 0 − 2 r + l − 2 t + b − 2 n + f 1 ⎦ ⎥ ⎥ ⎤
透视投影是最常见的投影方式,符合近大远小的规律,平行线不再平行;
透视投影的景视体是一个以原点为锥点的截锥体(Frustum),我们首先将截锥体变换成立方体,再进行正交投影,就完成了透视投影的过程;变换过程要保证几条规律:将远平面挤压至与近平面大小相同,挤压过程中 f f f
有:
[ x ′ y ′ z ′ 1 ] = [ n x n y ? z ] \begin{bmatrix}
x'\\
y'\\
z'\\
1
\end{bmatrix}
=
\begin{bmatrix}
n x\\
n y\\
? \\
z
\end{bmatrix}
⎣ ⎢ ⎢ ⎡ x ′ y ′ z ′ 1 ⎦ ⎥ ⎥ ⎤ = ⎣ ⎢ ⎢ ⎡ n x n y ? z ⎦ ⎥ ⎥ ⎤
考虑 ? ? ?
对于远近平面上的两点,需要保证:
[ x y n 1 ] → [ n x n y n 2 n ] , [ x y f 1 ] → [ n x n y f 2 f ] \begin{bmatrix}
x\\
y\\
n\\
1
\end{bmatrix}
\to
\begin{bmatrix}
n x\\
n y\\
n^2 \\
n
\end{bmatrix}
,\\
\begin{bmatrix}
x\\
y\\
f\\
1
\end{bmatrix}
\to
\begin{bmatrix}
nx\\
ny\\
f^2 \\
f
\end{bmatrix}
⎣ ⎢ ⎢ ⎡ x y n 1 ⎦ ⎥ ⎥ ⎤ → ⎣ ⎢ ⎢ ⎡ n x n y n 2 n ⎦ ⎥ ⎥ ⎤ , ⎣ ⎢ ⎢ ⎡ x y f 1 ⎦ ⎥ ⎥ ⎤ → ⎣ ⎢ ⎢ ⎡ n x n y f 2 f ⎦ ⎥ ⎥ ⎤
得到了方程组:
{ A x + B y + C n + D = n 2 A x + B y + C f + D = f 2 \begin{cases}
Ax+By+Cn+D=n^2\\
Ax+By+Cf+D=f^2
\end{cases}
{ A x + B y + C n + D = n 2 A x + B y + C f + D = f 2
其中 x , y , n , f x,y,n,f x , y , n , f A , B , C , D A,B,C,D A , B , C , D A = 0 , B = 0 , C = n + f , D = − n f A=0,B=0,C=n+f,D=-nf A = 0 , B = 0 , C = n + f , D = − n f
则:
M p e r s p → o r t h o = [ n 0 0 0 0 n 0 0 0 0 n + f − n f 0 0 1 0 ] M_{persp\to ortho}=
\begin{bmatrix}
n&0&0&0\\
0&n&0&0\\
0&0&n+f&-nf\\
0&0&1&0
\end{bmatrix}
M p e r s p → o r t h o = ⎣ ⎢ ⎢ ⎡ n 0 0 0 0 n 0 0 0 0 n + f 1 0 0 − n f 0 ⎦ ⎥ ⎥ ⎤
即 M p e r s p = M o r t h o M p e r s p → o r t h o M_{persp}=M_{ortho}M_{persp\to ortho} M p e r s p = M o r t h o M p e r s p → o r t h o
实际在这种模型中,z z z
视角变换之后,所有的物体均已经变换至 [ − 1 , 1 ] 3 {[-1,1]}^3 [ − 1 , 1 ] 3
宽高比 aspect_ratio=width/height ;
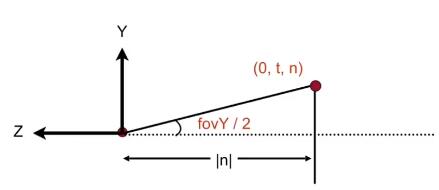
视角(field-of-view),fovY为垂直视场角,fovX为水平视场角,此课程中fov默认为垂直视场角;
在视角变换之后,相机位于原点, y + y^{+} y + z − z^{-} z − l = − r , b = − t l=-r,b=-t l = − r , b = − t
考虑 fovY 、aspect_ratio 与 l, r, b, t 的关系,如图所示:
tan f o v Y 2 = t ∣ n ∣ a s p e c t = r t \tan\frac{fovY}2=\frac t{|n|}\\
aspect=\frac r t
tan 2 f o v Y = ∣ n ∣ t a s p e c t = t r
我们将屏幕视为二维数组,光栅化(rasterize)即为在屏幕上绘制的过程;
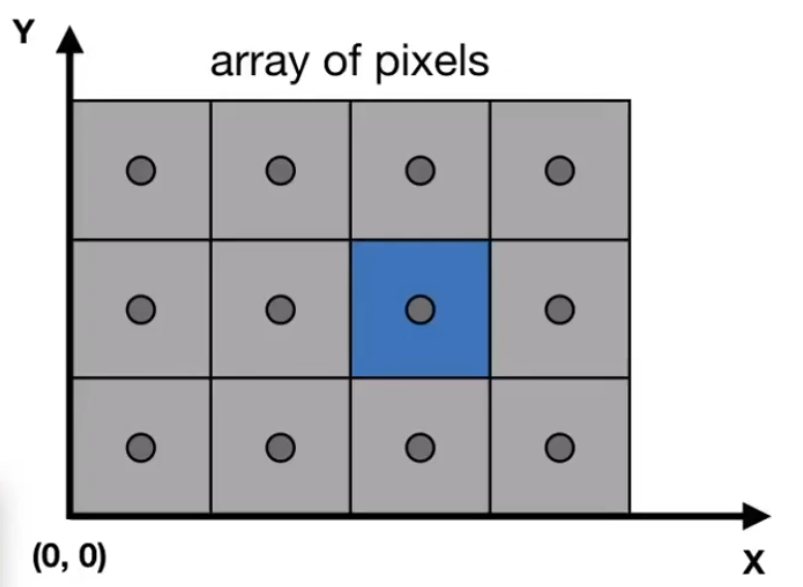
此课程中规定,屏幕空间的像素坐标视作分别代表X、Y轴位置的整数数对,如下图蓝色位置为 (2,1) ;
对于 width × height \text {width}\times \text{height} width × height
虽然像素坐标为整数坐标,但是坐标为 (x, y) 的像素中心在 (x+0.5, y+0.5) ;
屏幕覆盖范围为 (0, 0) 到 (width, height) ;
我们需要完成从 [ − 1 , 1 ] 3 {[-1,1]}^{3} [ − 1 , 1 ] 3 [ 0 , w i d t h ] × [ 0 , h e i g h t ] [0,width]\times[0,height] [ 0 , w i d t h ] × [ 0 , h e i g h t ]
我们先不考虑 z 坐标,将 xy 坐标拉伸至屏幕范围,有视口变换矩阵:
M v i e w p o r t = [ w i d t h 2 0 0 w i d t h 2 0 h e i g h t 2 0 h e i g h t 2 0 0 1 0 0 0 0 1 ] M_{viewport}=
\begin{bmatrix}
\frac {width}2&0&0&\frac {width}2\\
0&\frac {height}2&0&\frac {height}2\\
0&0&1&0\\
0&0&0&1
\end{bmatrix}
M v i e w p o r t = ⎣ ⎢ ⎢ ⎡ 2 w i d t h 0 0 0 0 2 h e i g h t 0 0 0 0 1 0 2 w i d t h 2 h e i g h t 0 1 ⎦ ⎥ ⎥ ⎤
三角形存在很多独特的性质:
保证共面(guaranteed to be planar);
保证凸形,便于判断内外(well-defined interior);
利用重心坐标系便于插值以实现渐变(barycentric interpolation);
接下来我们首先考虑三角形的光栅化;
定义布尔函数 inside(tri, x, y) ,其中xy不要求整数,含义为:
inside ( t r i , x , y ) = { 1 ( x , y ) in triangle t r i 0 otherwise \text{inside}(tri,x,y)=
\begin{cases}
1&(x,y) \text{ in triangle }tri\\
0&\text{otherwise}
\end{cases}
inside ( t r i , x , y ) = { 1 0 ( x , y ) in triangle t r i otherwise
1 2 3 for (int x = 0 ; x < xmax; ++x)for (int y = 0 ; y < ymax; ++y)inside (tri, x + 0.5 , y + 0.5 );
可以用同侧法判断点是否在三角形内;
关于点在边界上的情况,按统一标准处理即可;
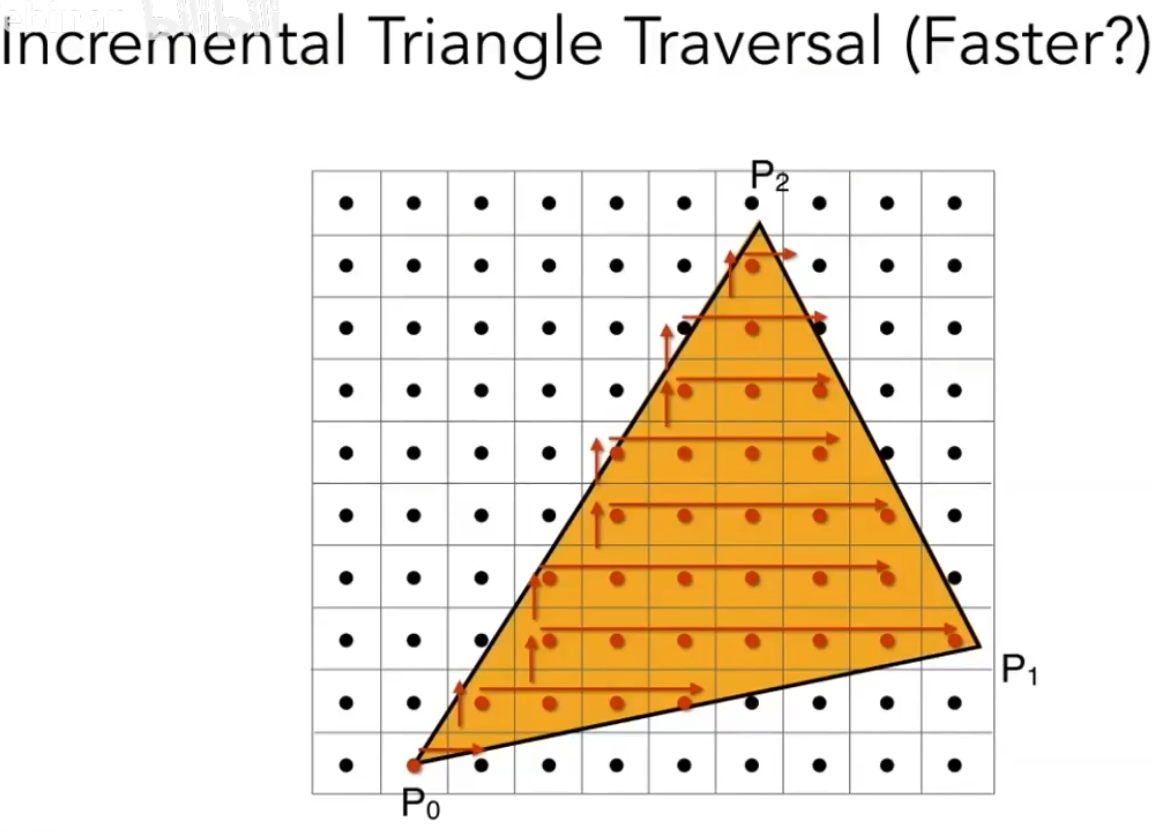
考虑枚举所有像素的低效,我们可以只扫描三角形轴向包围盒(axis-aligned bounding box,AABB)中的像素([ X m i n , X m a x ] × [ Y m i n , Y m a x ] [X_{min},X_{max}]\times[Y_{min},Y_{max}] [ X m i n , X m a x ] × [ Y m i n , Y m a x ]
对于细长且旋转的三角形,AABB 策略会被降低效率,可以使用增量遍历策略:
走样:CG中不符合预期的采样(Sampling Artifacts (Errors/Mistakes/Inaccuracies) in Computer Graphics),包括锯齿、摩尔纹、车轮效应等;
对于余弦函数,我们称满足 cos 2 π f x \cos2\pi fx cos 2 π f x f f f
同样采样方法采样两种不同频率的信号出现相同的信息称之为走样;
滤波即为去掉某些频率的内容;
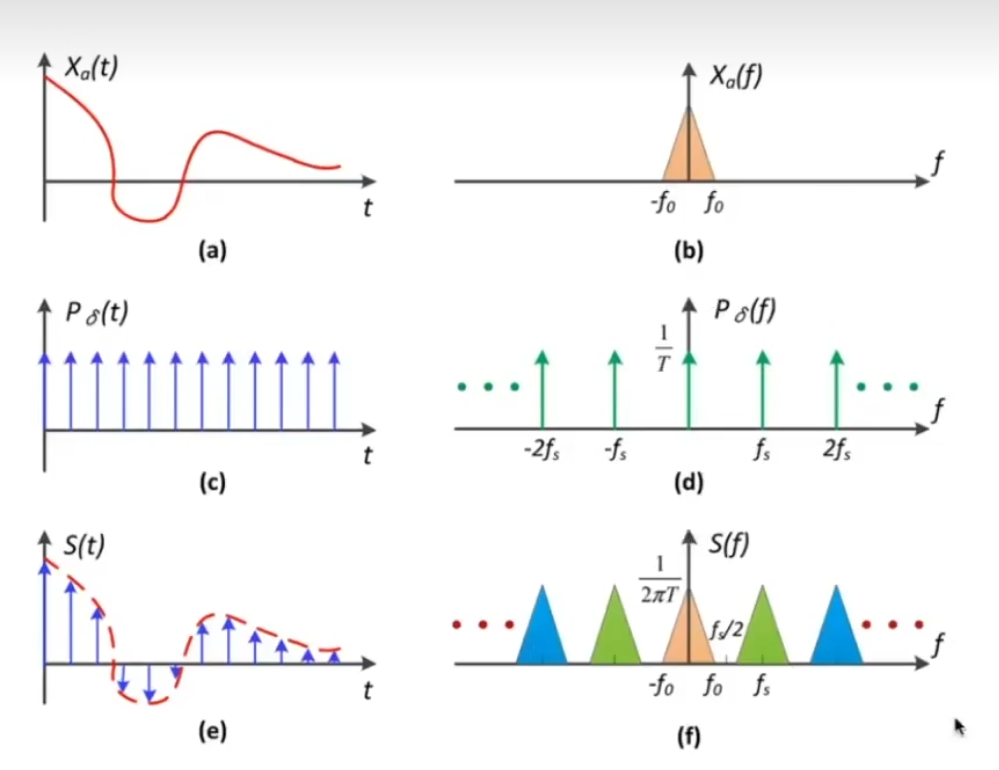
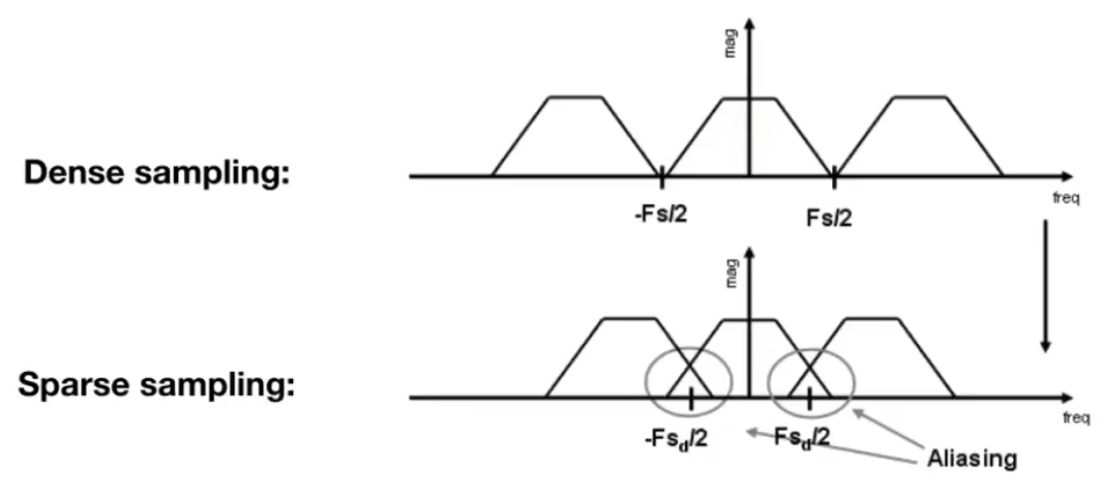
时域上的乘积等于频域上的卷积,所以采样就是重复原始信号的频谱;
如果采样率不足(fs较小)或高频丰富(f0较大)时,便会发生频谱混叠(aliasing),即为走样;
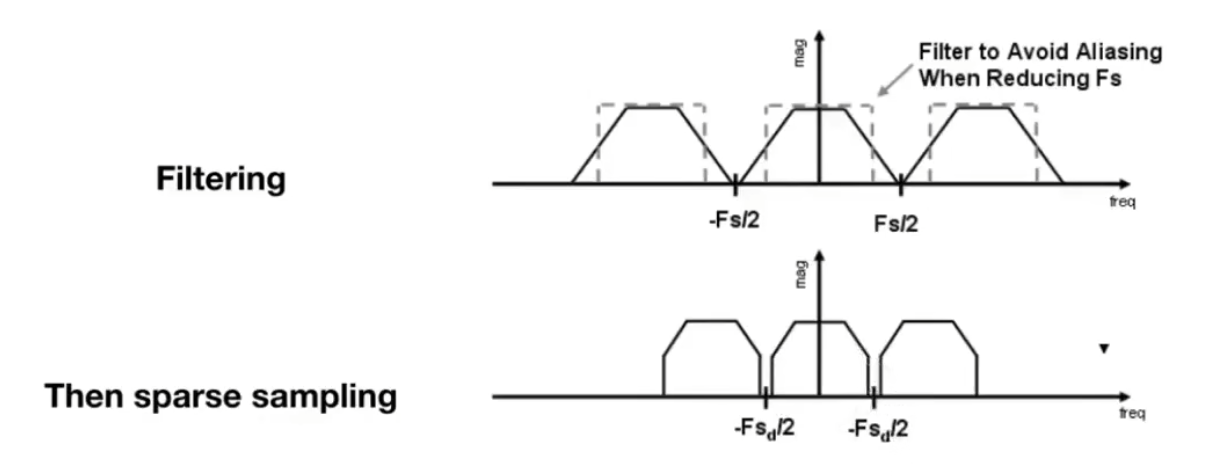
进一步说,除了增加采样率 外,还可以通过先低通滤波再采样 的方法;
在实际操作中,我们通过对inside函数进行卷积来实现低通滤波,理想情况下,inside函数可以返回像素面积中被三角形覆盖的比例,实际实现上有以下几种途径:
超采样(Super-Sample Anti-Aliasing,SSAA)
我们将每个像素划分为更多小的像素,分别对小像素进行采样后进行平均;
多重采样(Multi-Sample AA,MSAA)
不同于SSAA,SSAA对于所有子采样点着色,而MSAA只对当前模型所更新的子采样点进行着色;
SSAA与MSAA都需要进行解析(Resolve),信号必须重新采样到指定的分辨率,这样我们才可以显示它;
SSAA和MSAA会大量消耗算力,实际实现上可能通过不规则分布和像素复用等方法降低消耗;
快速近似(Fast Approximate AA,FXAA)
在光栅化后带锯齿的图像上寻找边界,将边界替换为没有锯齿的边界;
时域抗锯齿(Temporal AA,TAA)
类似于在时域上进行多重采样;
深度学习超分辨率(Deep Learning Super Sampling,DLSS)
从远到近绘制,近的物体覆盖远的物体;
同距离物体的绘制顺序并不随意,会出现遮挡问题:
也可能出现无法解决的深度组合:
所以实际解决时无法使用此算法;
为了简单起见,此部分我们认为 z 总是正的,z 越小物体离相机越近
在渲染图像时同时生成两个结果:对于想要的图像存储在 frame buffer ,对于每个像素的深度信息存储在 depth buffer;
深度缓存对于每个像素,只维护此帧中最小的 z 值;
1 2 3 4 5 6 7 8 9 lnitialize depth buffer to ∞;sample (x,y,z) in T)if (z < zbuffer[x,y]) else
由画家算法的 O ( n log n ) O(n\log n) O ( n log n ) O ( n ) O(n) O ( n )
在 MSAA 策略下,z-buffer 粒度会上升至每一个采样点;
z-buffer 不能处理透明物体的深度问题;
着色:对不同物体应用不同材质(material)的过程;
将从一个点接受的光分为三部分:镜面反射(specular highlights)、漫反射(diffuse reflection)、环境光(ambient lighting);环境光实际上是由环境和周边物体的反射混合形成的,在此模型中被简化为一个常量;
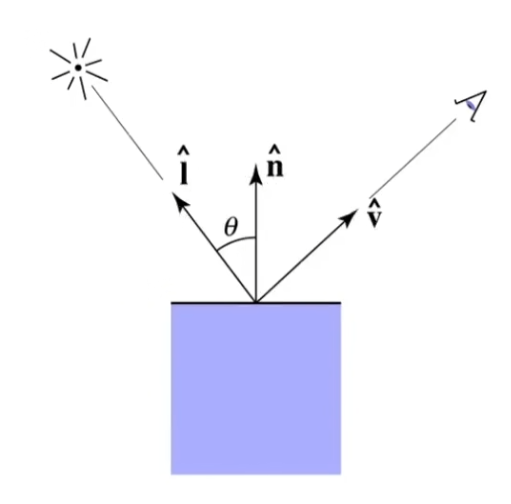
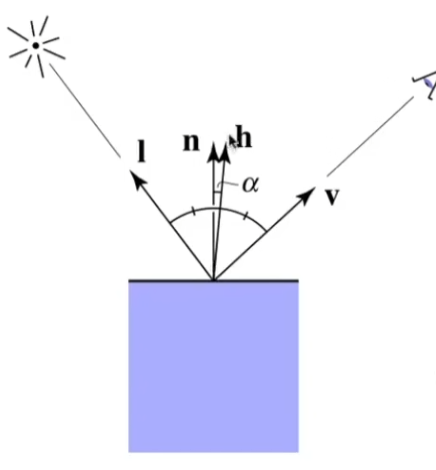
有如下输入量:相机方向单位向量 v ^ \hat v v ^ n ^ \hat n n ^ l ^ \hat l l ^ k k k
模型是一种局部光照模型,指只考虑着色点、相机和光源之间的关系,不考虑着色点是否被其他物体遮挡;
对于漫反射项 L d L_d L d L s L_s L s L a L_a L a
L = L d + L s + L a L=L_d+L_s+L_a
L = L d + L s + L a
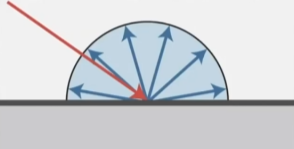
漫反射指对于一条打向着色点的光线,其被均匀地反射到各个方向;
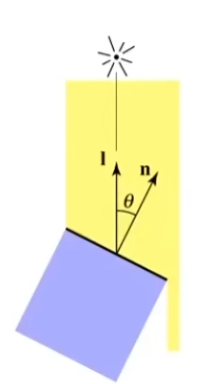
朗伯余弦定律(Lambert’s cosine law):单位面积接受的辐射能量与法向和光向的夹角有关,夹角有 cos θ = l ^ ⋅ n ^ \cos\theta =\hat l\cdot \hat n cos θ = l ^ ⋅ n ^
光衰减(平方反比定律):与点光源距离为1的单位面积接受的能量为 I ,则距离为 r 的单位面积接受的能量为 I / r 2 I/r^2 I / r 2
综上有漫反射光公式
L d = k d ( I / r 2 ) max ( 0 , n ^ ⋅ l ^ ) L_d=k_d(I/r^2)\max(0,\hat n\cdot \hat l)
L d = k d ( I / r 2 ) max ( 0 , n ^ ⋅ l ^ )
漫反射光强 = 漫反射系数 * 原始光强/(光源距离^2 )* cos法光角;
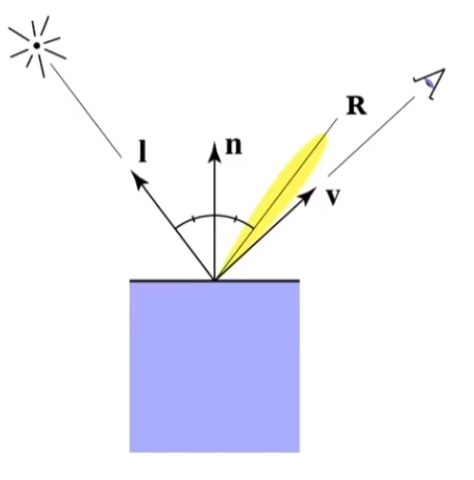
v ^ \hat v v ^ v ^ \hat v v ^ h ^ \hat h h ^ v ^ \hat v v ^ l ^ \hat l l ^ n ^ \hat n n ^
有
h ^ = bisector ( v , l ) = v ^ + l ^ ∣ ∣ v ^ + l ^ ∣ ∣ L s = k s ( I / r 2 ) max ( 0 , cos α ) p = k s ( I / r 2 ) max ( 0 , n ^ ⋅ h ^ ) p \hat h=\text{bisector}(v,l)\\
=\frac{\hat v+\hat l}{||\hat v+\hat l||}\\
L_s=k_s(I/r^2)\max(0,\cos\alpha)^p\\
=k_s(I/r^2)\max(0,\hat n\cdot \hat h)^p
h ^ = bisector ( v , l ) = ∣ ∣ v ^ + l ^ ∣ ∣ v ^ + l ^ L s = k s ( I / r 2 ) max ( 0 , cos α ) p = k s ( I / r 2 ) max ( 0 , n ^ ⋅ h ^ ) p
镜面反射光强 = 镜面反射系数 * 原始光强/(光源距离^2 )* cos法半角;
通常认为高光为白色,镜面反射系数取白色光反射系数;
朗伯余弦定律在镜面反射项中被简化;
如果通过 R 与 v ^ \hat v v ^
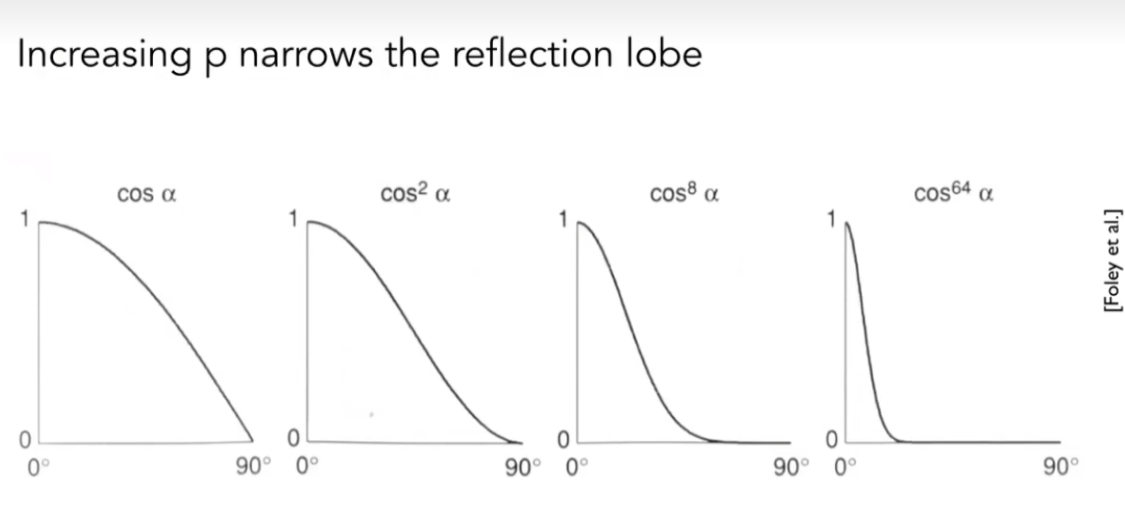
上式中的 p p p
L a = k a I a L_a=k_aI_a
L a = k a I a
此模型中环境光与光向、法向、视向无关,视作一常数;
如果一个点不在阴影中,那么说明这个点对于相机和光源都是可见的;
阴影映射用于处理单个点光源的二值硬阴影(软阴影越靠近物体边界越浅,来自于光源非点产生的半影);
在点光源处放置一个摄像机,对场景光栅化,存储每个可见点(与光源)的深度信息(Z-buffer);
从相机出发再次光栅化,对于可见点将其投影回光源判断其深度与存储值是否一致,一致即说明该点无阴影,不一致即说明该点在阴影下;
阴影映射本身受制于点光源处光栅化的分辨率,生成的阴影会包含锯齿;
着色频率是指空间上进行着色的密度,有以下几种主要方法:
平面着色(flat shading)
对于每个三角形进行着色计算,将结果应用于整个三角形上;
顶点着色(gouraud shading)
对于每个顶点进行着色计算,三角形内的着色由插值得出;
像素着色(Phong shading)与布林-冯模型的冯是同一个人,与着色模型无关
对于每个像素进行着色计算;
在面数较少时,像素着色频率越高效果越逼真,但在高面数情况下效果相近;
如果已知模型的原始几何属性(e.g. 球、平面等),可以直接通过几何方法计算法线;
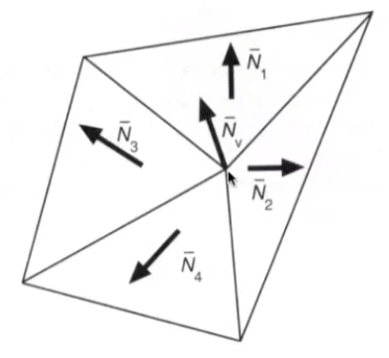
一般情况,可以认为顶点法线是其相邻面法线的平均值
N v = ∑ N i ∣ ∣ ∑ N i ∣ ∣ N_v=\frac {\sum N_i}{||\sum N_i||}
N v = ∣ ∣ ∑ N i ∣ ∣ ∑ N i
为了获取更准确的法线,可以按三角形面积等进行加权平均;
像素的法线可以通过重心插值获取;
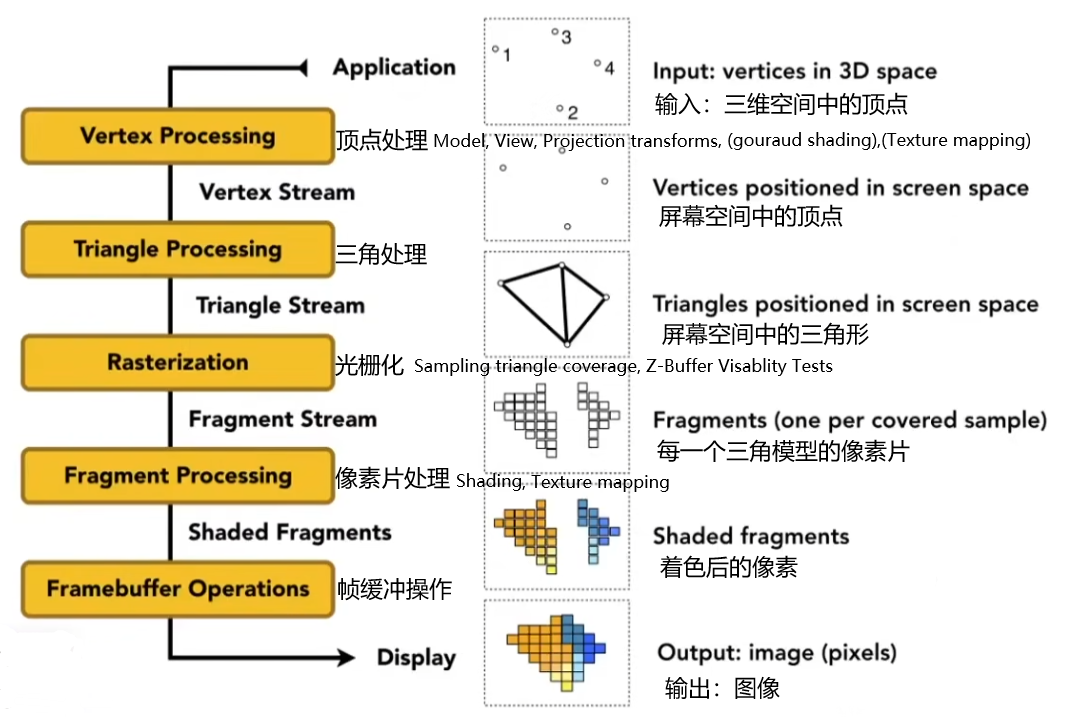
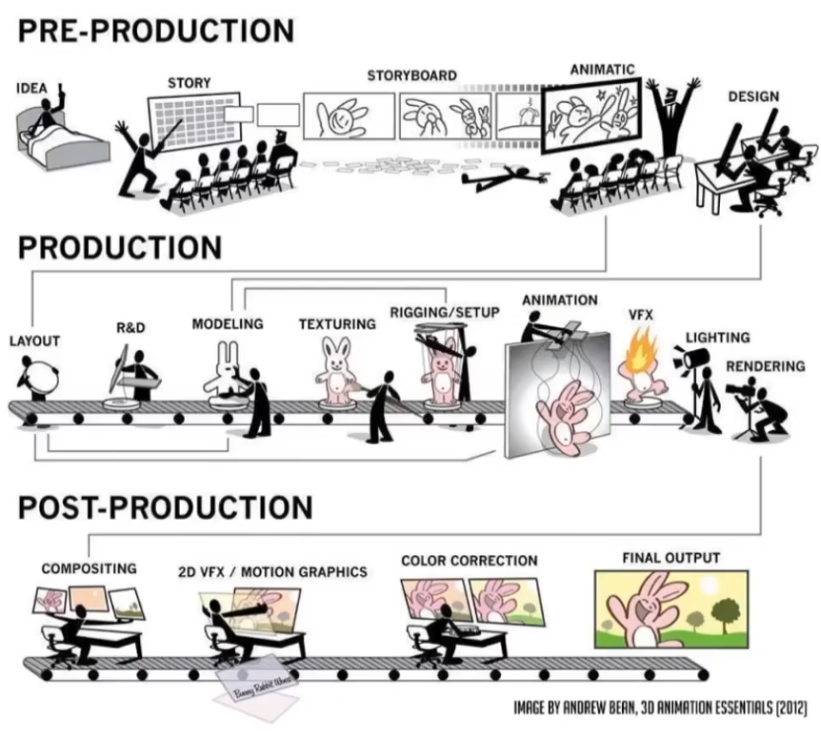
实时渲染管线指从场景到图像的过程;
http://shadertoy.com/view/Id3Gz2
三维物体的表面是二维的,表面可以与一张图形成映射关系;我们可以定义一张图,图上的每个三角形都映射到模型上的三角形,图上三角形的纹理就代表了模型上对应三角形的纹理;这张图就是uv贴图,得名于其两个坐标轴一般用 u 和 v 表示,无论其是方形或是矩形,通常认为范围有 u , v ∈ [ 0 , 1 ] u,v\in[0,1] u , v ∈ [ 0 , 1 ]
如果一块纹理在映射时,与上下左右的自己衔接不会产生缝隙,则被称为四方连续(tilable texture);
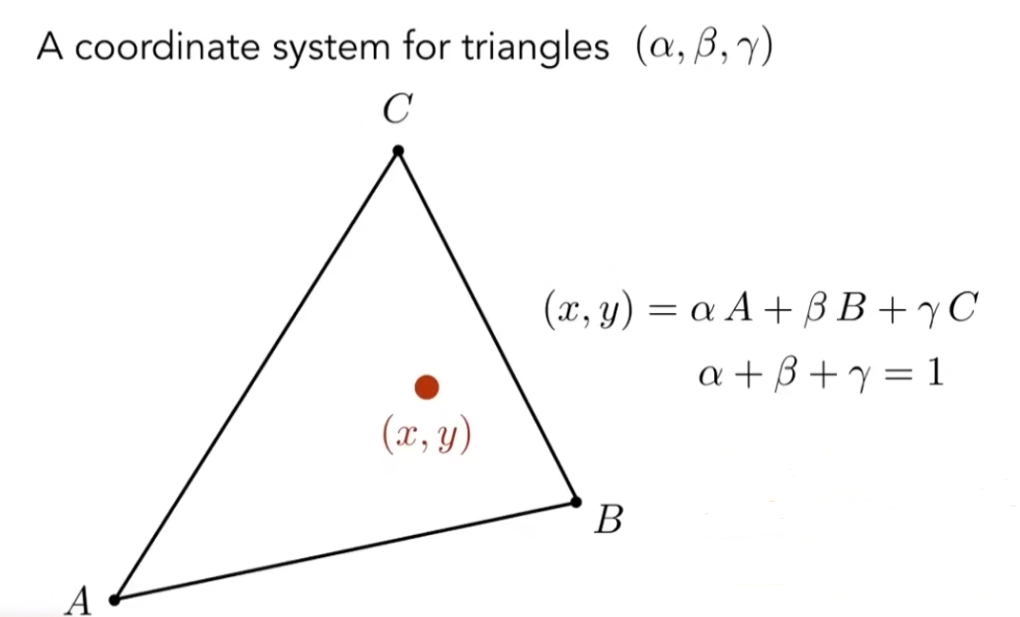
我们假设已经掌握了这种映射关系,在已知三角形顶点坐标的情况下,获取三角形内部点的坐标需要通过重心坐标(Barycentric Coordinates)来完成;
重心坐标可以用于三角形内部的插值,在顶点处处理出的值(纹理映射、颜色、法向等)可以平滑地过渡到三角形内的任何一点;
在 △ A B C \triangle ABC △ A B C ( x , y ) (x,y) ( x , y )
由于和等于1的限制,实际上坐标由两个参数即可描述;
如果点在三角形内,则有 α , β , γ ⩾ 0 \alpha ,\beta, \gamma\geqslant0 α , β , γ ⩾ 0
对于平面内任意一点 P ,考虑 △ P A C , △ P C B , △ P B A \triangle PAC,\triangle PCB, \triangle PBA △ P A C , △ P C B , △ P B A A B , A A , A C A_B, A_A, A_C A B , A A , A C
α P = A A A A + A B + A C β P = A B A A + A B + A C γ P = A C A A + A B + A C \alpha_P=\frac {A_A}{A_A+A_B+A_C}\\
\beta_P=\frac {A_B}{A_A+A_B+A_C}\\
\gamma_P=\frac {A_C}{A_A+A_B+A_C}
α P = A A + A B + A C A A β P = A A + A B + A C A B γ P = A A + A B + A C A C
从坐标角度考虑,对于平面内任意一点 P ( x , y ) P(x,y) P ( x , y )
α P = − ( x − x B ) ( y C − y B ) + ( y − y B ) ( x C − x B ) − ( x A − x B ) ( y C − y B ) + ( y A − y B ) ( x C − x B ) β P = − ( x − x C ) ( y A − y C ) + ( y − y C ) ( x A − x C ) − ( x B − x C ) ( y A − y C ) + ( y B − y C ) ( x A − x C ) γ P = 1 − α P − β P \alpha_P=\frac{-(x-x_B)(y_C-y_B)+(y-y_B)(x_C-x_B)}{-(x_A-x_B)(y_C-y_B)+(y_A-y_B)(x_C-x_B)}\\
\beta_P=\frac{-(x-x_C)(y_A-y_C)+(y-y_C)(x_A-x_C)}{-(x_B-x_C)(y_A-y_C)+(y_B-y_C)(x_A-x_C)}\\
\gamma_P=1-\alpha_P-\beta_P
α P = − ( x A − x B ) ( y C − y B ) + ( y A − y B ) ( x C − x B ) − ( x − x B ) ( y C − y B ) + ( y − y B ) ( x C − x B ) β P = − ( x B − x C ) ( y A − y C ) + ( y B − y C ) ( x A − x C ) − ( x − x C ) ( y A − y C ) + ( y − y C ) ( x A − x C ) γ P = 1 − α P − β P
△ A B C \triangle ABC △ A B C ( 1 3 , 1 3 , 1 3 ) (\frac 13,\frac 13,\frac 13) ( 3 1 , 3 1 , 3 1 )
对于三角形内一点 P ( α , β , γ ) P(\alpha,\beta,\gamma) P ( α , β , γ ) V A , V B , V C V_A,V_B,V_C V A , V B , V C V P = α V A + β V B + γ V C V_P=\alpha V_A+\beta V_B+\gamma V_C V P = α V A + β V B + γ V C
在投影变换下,不能够保证重心坐标不变;需要在三维空间进行插值,或对插值结果需要进行矫正;参考资料
1 z 0 = α 1 z 1 + β 1 z 2 + γ 1 z 3 b 0 z 0 = α b 1 z 1 + β b 2 z 2 + γ b 3 z 3 \frac 1{z_0}=\alpha\frac 1{z_1}+\beta\frac 1{z_2}+\gamma\frac 1{z_3}\\
\frac {b_0}{z_0}=\alpha\frac {b_1}{z_1}+\beta\frac {b_2}{z_2}+\gamma\frac {b_3}{z_3}
z 0 1 = α z 1 1 + β z 2 1 + γ z 3 1 z 0 b 0 = α z 1 b 1 + β z 2 b 2 + γ z 3 b 3
其中 b 0 b_0 b 0 b 1 , b 2 , b 3 b_1,b_2,b_3 b 1 , b 2 , b 3 z 0 z_0 z 0 [ α , β , γ ] [\alpha,\beta,\gamma] [ α , β , γ ] z 1 , z 2 , z 3 z_1,z_2,z_3 z 1 , z 2 , z 3
1 2 3 4 for each rasterized screen sample (x,y): texture coordinate at (x,y); texture .sample (u,v);sample 's color to texcolor;
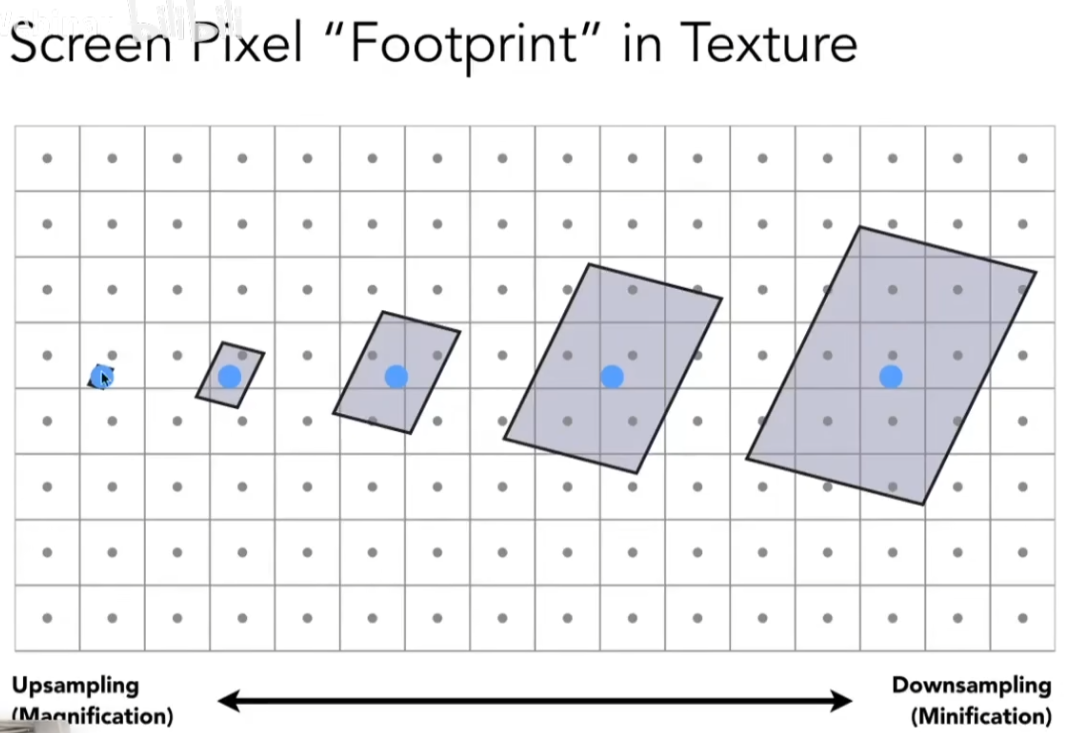
一个像素与一个纹理元素(texel)(纹理像素)的大小关系并不固定,需要进行“纹理缩放”;
如果纹理分辨率低于渲染所需的分辨率,就会产生不符合预期的效果;
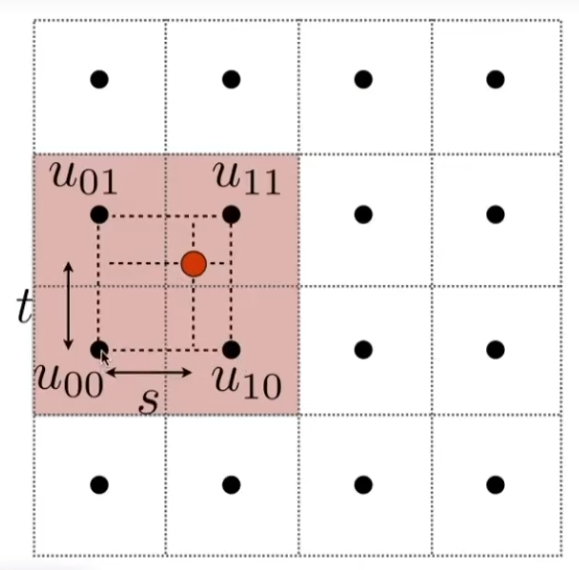
对于计算出来的浮点 ( u , v ) (u,v) ( u , v )
红点为计算出的 ( u , v ) (u,v) ( u , v )
定义一个运算:线性插值(linear interpolation),对于 x ∈ [ 0 , 1 ] x\in[0,1] x ∈ [ 0 , 1 ] v 1 , v 0 v_1,v_0 v 1 , v 0
lerp ( x , v 0 , v 1 ) = v 0 + x ( v 1 − v 0 ) \text{lerp}(x,v_0,v_1)=v_0+x(v_1-v_0)
lerp ( x , v 0 , v 1 ) = v 0 + x ( v 1 − v 0 )
对双线性插值,定义有
u 0 = lerp ( s , u 00 , u 10 ) u 1 = lerp ( s , u 01 , u 11 ) u u v = lerp ( t , u 0 , u 1 ) u_0=\text{lerp}(s,u_{00},u_{10})\\
u_1=\text{lerp}(s,u_{01},u_{11})\\
u_{uv}=\text{lerp}(t,u_{0},u_{1})
u 0 = lerp ( s , u 0 0 , u 1 0 ) u 1 = lerp ( s , u 0 1 , u 1 1 ) u u v = lerp ( t , u 0 , u 1 )
双立方插值(Bicubic)区别在于考虑邻近的16个纹素进行立方插值;
如果一个纹素的大小远小于一个像素的大小,那么便会产生走样现象,可以通过反走样方法进行处理,但是比较耗费资源,这里使用另一种策略;
我们将像素范围内的纹素近似平均值作为返回值;
Mipmap是一种一种快速的、近似的、正方形的范围查询;
我们需要存储纹理图的低分辨率版本(每级边长折半,多花费1/3的空间);
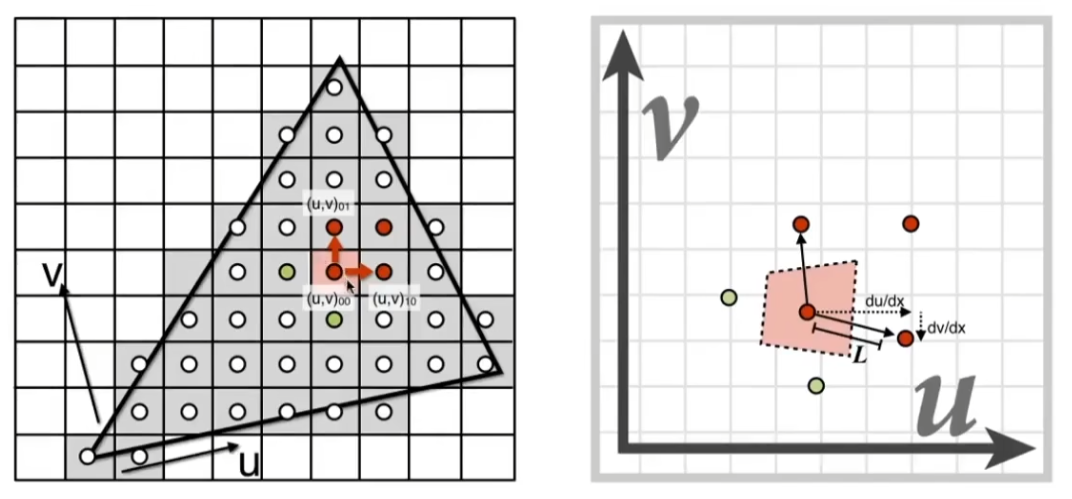
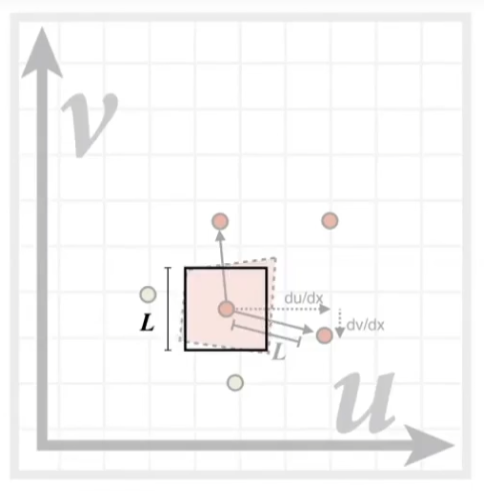
接下来计算单个像素的覆盖面积:考虑一个采样点和其水平、垂直方向的两个相邻采样点,这三个点映射在纹理图上的坐标;
L = max ( ( d u d x ) 2 + ( d v d x ) 2 , ( d u d y ) 2 + ( d v d y ) 2 ) L=\max(\sqrt{(\frac {du}{dx})^2+(\frac {dv}{dx})^2},\sqrt{(\frac {du}{dy})^2+(\frac {dv}{dy})^2})
L = max ( ( d x d u ) 2 + ( d x d v ) 2 , ( d y d u ) 2 + ( d y d v ) 2 )
L 即可被近似为像素所在纹理上正方形的边长;
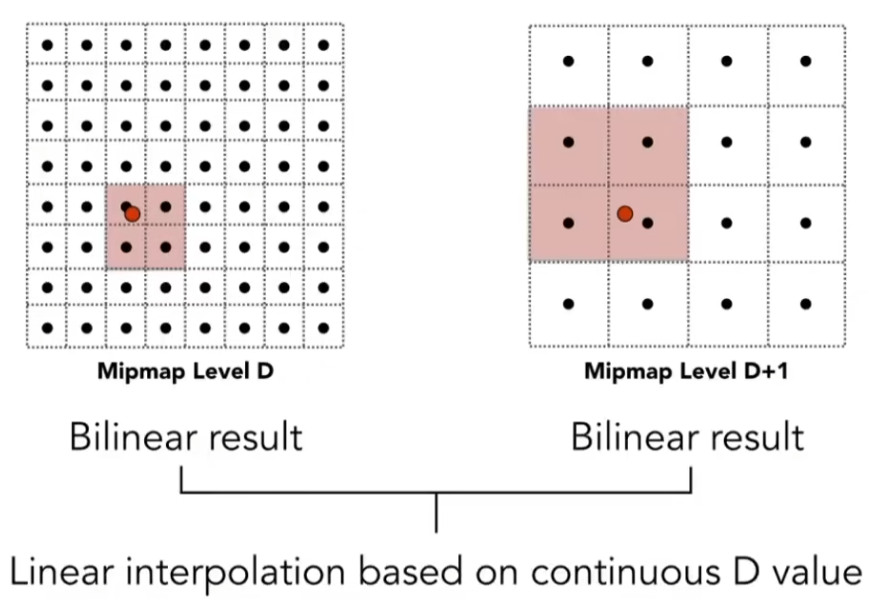
Mipmap级数 D 有 D = log 2 L D=\log_2L D = log 2 L
对于非整数的 D ,我们可以对 Mipmap 进行层间插值,这个过程被称为三线性插值(水平,垂直,层间);
Mipmap 会产生 Overblur (过度模糊)现象,由于在方形确定和三线性插值过程中使用了大量的近似;
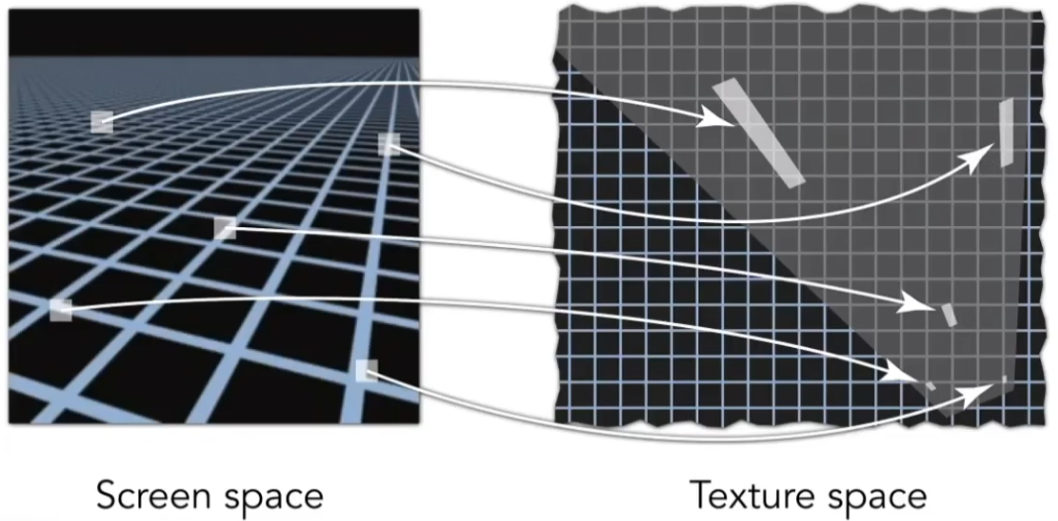
各向异性指在各个方向上其表现不同,在这里特指两个轴向方向上的表现不同;
各向异性过滤可以解决上图中的轴向矩形区域,对于斜向区域仍然存在问题;
不同于 Mipmap 只存储了上图中对角线上的图片,各向异性过滤通过存储不同长宽比的原始图像来实现轴向矩形区域的查询(多花费3倍的空间);
各向异性过滤的层数选项:对于4x各向异性过滤指取上图左上 3 × 3 3\times3 3 × 3
更进一步可以使用 EWA 过滤(EWA filtering)来实现真正意义上的各向同性,在此不作赘述;
在现代 GPU 中,纹理可以抽象地被表述成可以快速进行范围查询的一块数据;
如果我们通过纹理来描述环境光情况,再用这个纹理对物体进行渲染,便可以实现环境光照的效果;通过此种方法进行模拟,需要假设环境光来自无限远;
假设有一个镜子的球,将球面上反射的环境光记录为环境光信息,这就是球环境贴图(Spherical Environment Map);
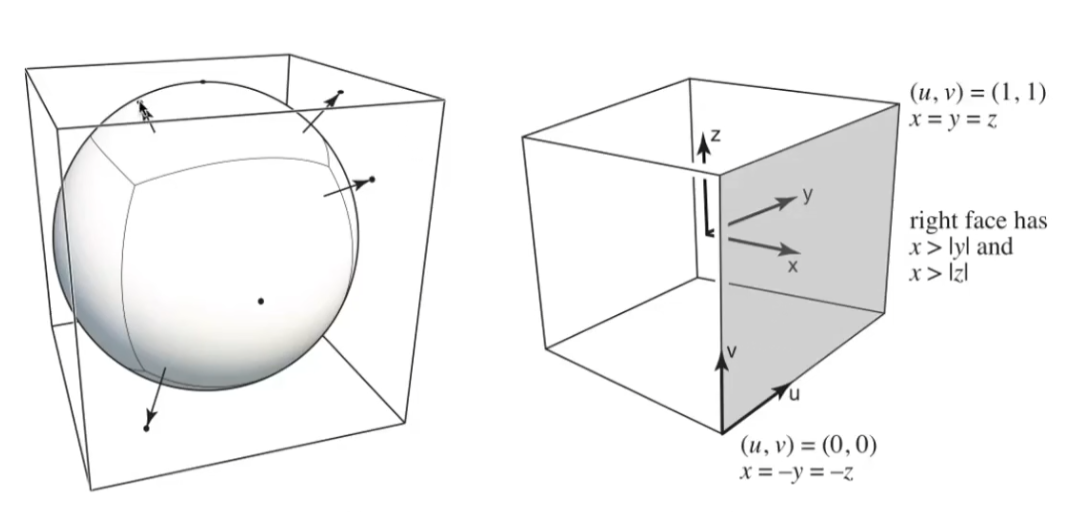
接下来对球面进行展开存储,在类似于世界地图的投影方式中,两极部分会被扭曲变形;考虑使用立方体贴图(Cube Map)进行存储:
在球外添加一个正方体包围盒,从球心发出的射线打到包围盒上的位置即为该方向上的球面映射到立方体贴图上的位置;
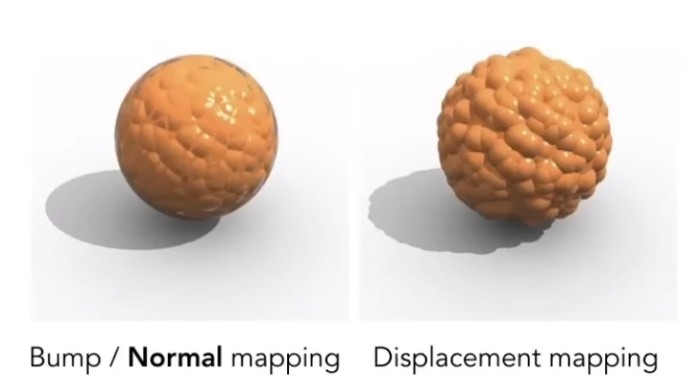
纹理不止可以描述颜色,如果通过纹理记录表面相对高度,便可以在不增加面数的情况下来定义更精细的(假)模型;
假设有法线贴图 p = h ( u , v ) p=h(u,v) p = h ( u , v ) ( u , v ) (u,v) ( u , v ) ( 0 , 0 , 1 ) (0,0,1) ( 0 , 0 , 1 )
d p d u = c 1 [ h ( u + 1 , v ) − h ( u , v ) ] d p d v = c 1 [ h ( u , v + 1 ) − h ( u , v ) ] n ^ = ( − d p d u , − d p d v , 1 ) . normalized() \frac {dp}{du}=c_1[h(u+1,v)-h(u,v)]\\
\frac {dp}{dv}=c_1[h(u,v+1)-h(u,v)]\\
\hat n=(-\frac {dp}{du},-\frac {dp}{dv},1).\text{normalized()}
d u d p = c 1 [ h ( u + 1 , v ) − h ( u , v ) ] d v d p = c 1 [ h ( u , v + 1 ) − h ( u , v ) ] n ^ = ( − d u d p , − d v d p , 1 ) . normalized()
c1,c2为在u,v两个方向上的影响系数,代表纹理定义的法线对于展示物体法线的影响系数;
由于原始法线 ( 0 , 0 , 1 ) (0,0,1) ( 0 , 0 , 1 )
参考资料
TBN矩阵指的是由切线(Tangent)、副切线(Bitangent)(有些地方也叫副法线)、法线(Normal),组成的3x3的矩阵(这里的切线、副切线、法线全部指的是世界空间的向量,不是切线空间下的,TBN三向量正交且归一);
参考作业代码,有
T = [ N x N y N x 2 + N z 2 N x 2 + N z 2 N y N z N x 2 + N z 2 ] B = N × T T=
\begin{bmatrix}
\frac{N_xN_y}{\sqrt{N_x^2+N_z^2}}\\
\sqrt{N_x^2+N_z^2}\\
\frac{N_yN_z}{\sqrt{N_x^2+N_z^2}}
\end{bmatrix}\\
B=N\times T
T = ⎣ ⎢ ⎢ ⎡ N x 2 + N z 2 N x N y N x 2 + N z 2 N x 2 + N z 2 N y N z ⎦ ⎥ ⎥ ⎤ B = N × T
变换过程有
n W o r l d = [ T x B x N x T y B y N y T z B z N z ] n T B N n_{World}=
\begin{bmatrix}
T_x & B_x & N_x\\
T_y & B_y & N_y\\
T_z & B_z & N_z
\end{bmatrix}
n_{TBN}
n W o r l d = ⎣ ⎡ T x T y T z B x B y B z N x N y N z ⎦ ⎤ n T B N
相比于法线贴图只是修饰法线的结果,位移贴图是对顶点位置的移动;
观察边缘和阴影:
其代价为要求模型本身面数足够;为了解决这个问题 DirectX 使用动态曲面细分降低消耗;
三维程序化噪声(3D Procedural Noise)
预计算着色(Precomputed Shading)、环境光遮蔽纹理(Ambient occlusion texture map)
体渲染(Volume Rendering)
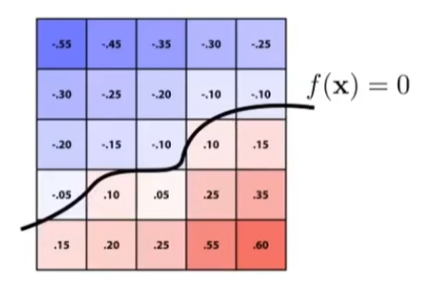
隐式(Implicit)描述是通过描述点之间关系来规定点的属性,比如三维空间中满足 x^2+y^2+z^2=1 的点的集合 ;更一般地定义为满足 f(x,y,z)=0 的点的集合 ;
隐式描述的缺点在于不直观,优点在于实现上可以快速判断给定点是否在指定集合中或是否在区域内/外;
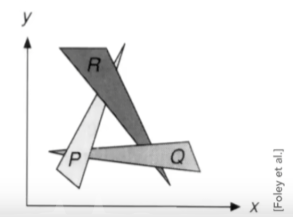
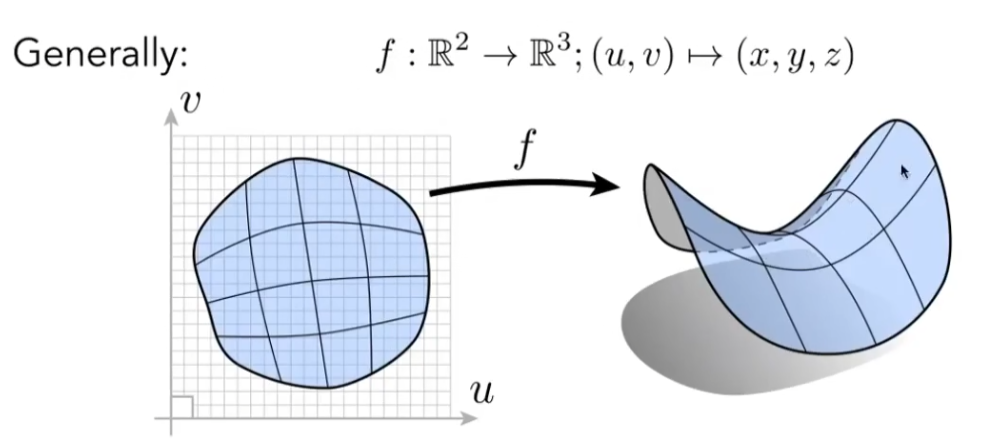
显式(Explicit)描述是指所有点都是直接定义或者通过参数映射得到的(参数映射如下图);
相比于隐式描述,显式描述的优点在于能够快速确定有哪些点在指定集合中,缺点在于难以判断点在区域内/外;
表面是有关 x ,y ,z 的多项式的零点集合;
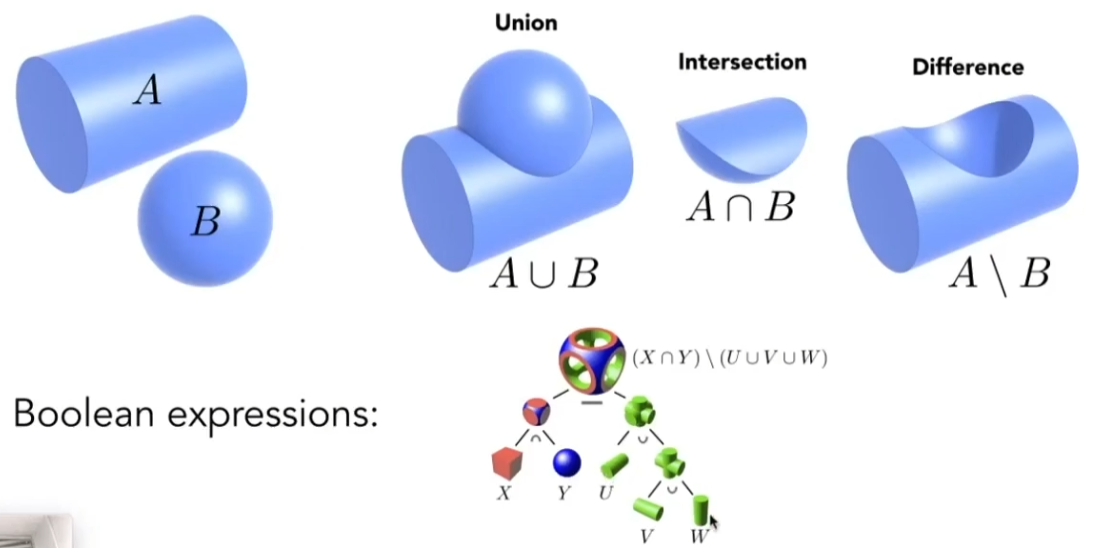
通过基本几何体的布尔(集合?)运算来定义更复杂的几何体;
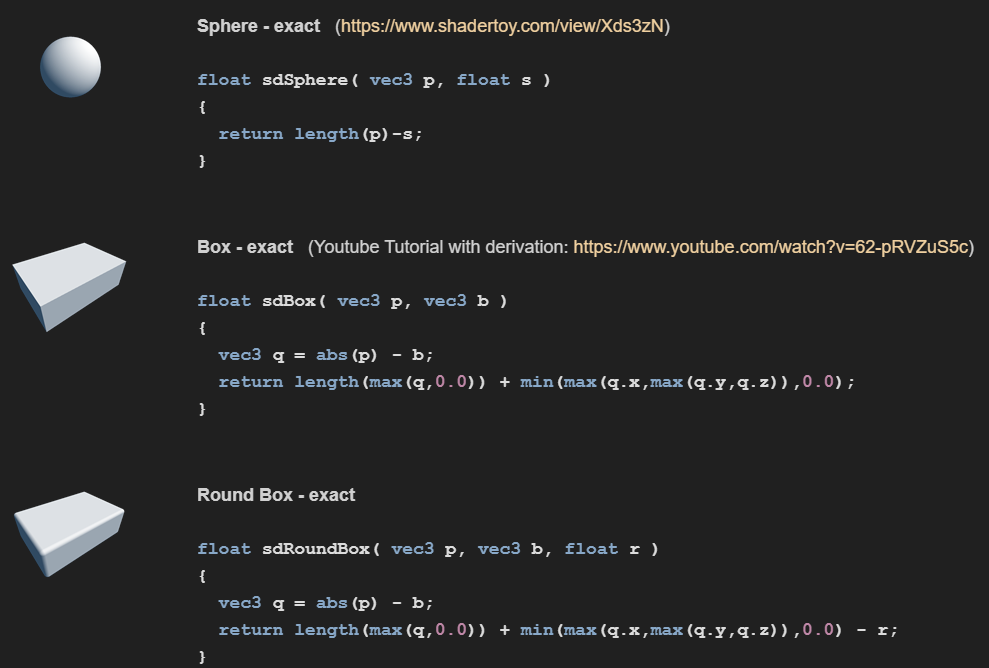
通过定义距离函数描述空间上任何一点到几何体表面的最小(有向)距离来构造几何体;
距离函数可以通过函数运算来获得两个几何体的中值(混合);
类似于距离函数,水平集是将距离函数定义域离散化到网格中;
分型是一种自相似结构;
不考虑表面的连续性,将表面用表面上的足够多点表示;
通常用于大量数据的情况( point/pixel >>1 )
这种方式可以容易地表示任何类型的模型,但在样本密度低的部分难以绘制;
在处理时,点云经常被转换为多边形网格;
易于处理;一般通过三角形或四边形网格实现;
由于需要处理图形间的连接关系,需要更复杂的数据结构;
是图形学中最常见的表现形式;
只是一个指定顶点、法线、文本坐标及其连接性的文本文件;‘
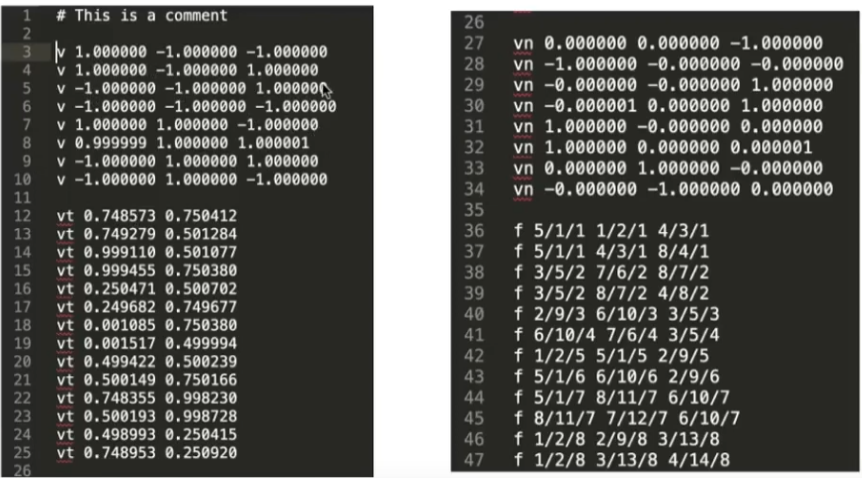
以下图为例,其中存储了一个正方体
其中 line 3-10 定义了8个顶点,line 12-25 定义了14个纹理坐标,line 27-34 定义了6个不同的平面法向量,line36-47定义了12个三角形,其中 4/3/1 含义为此处点坐标为4号,纹理坐标为3号,法线为1号 即为定义了使用第几个前述值;
用一系列的控制点去定义曲线;
对于 P 0 , . . P n + 1 P_0,..P_{n+1} P 0 , . . P n + 1
在 P 0 P_0 P 0 P n + 1 P_{n+1} P n + 1
在起点处切向为 n P 0 P 1 → n\overrightarrow{P_0P_1} n P 0 P 1 n P n P n + 1 → n\overrightarrow{P_{n}P_{n+1}} n P n P n + 1
对于曲线的仿射变换等于对控制点仿射变换后绘制曲线;(投影变换不属于仿射变换)
曲线在控制点形成的凸包内;
考虑已经给定的一系列控制点,如何绘制对应的贝塞尔曲线;
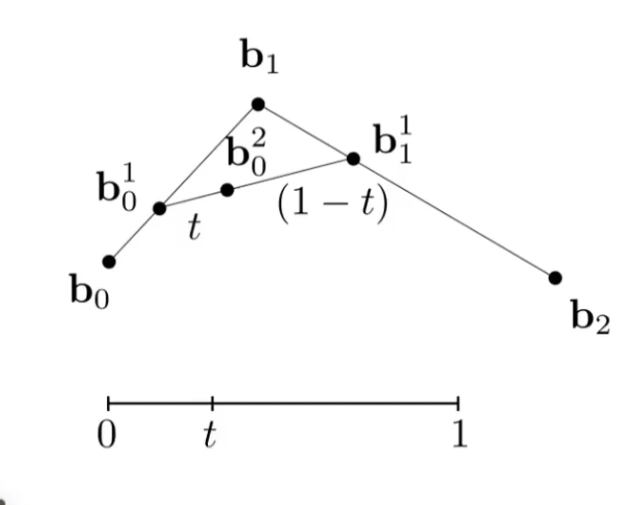
先将问题简化为三个点,此时生成的曲线为二阶贝塞尔曲线(quadratic Bezier);
对于曲线上参数为 t (t ∈ [ 0 , 1 ] t\in[0,1] t ∈ [ 0 , 1 ]
b 0 1 ( t ) = ( 1 − t ) b 0 + t b 1 b 1 1 ( t ) = ( 1 − t ) b 1 + t b 2 b 0 2 ( t ) = ( 1 − t ) b 0 1 + t b 1 1 b_0^1(t)=(1-t)b_0+tb_1\\
b_1^1(t)=(1-t)b_1+tb_2\\
b_0^2(t)=(1-t)b_0^1+tb_1^1
b 0 1 ( t ) = ( 1 − t ) b 0 + t b 1 b 1 1 ( t ) = ( 1 − t ) b 1 + t b 2 b 0 2 ( t ) = ( 1 − t ) b 0 1 + t b 1 1
足够精度在定义域内枚举 t 即可计算曲线;
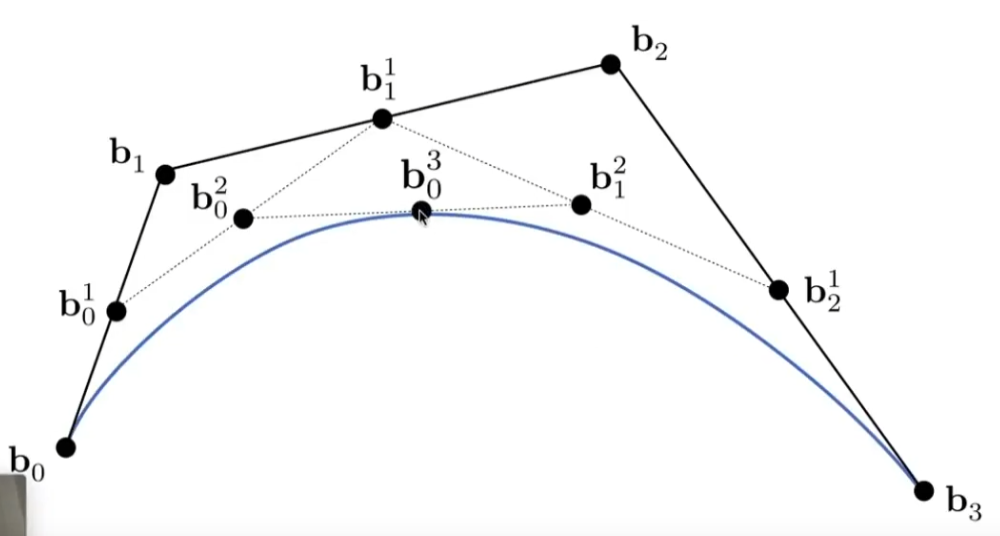
考虑四个点定义的贝塞尔曲线;
更广泛地,对于 n+1 个控制点(b 0 , . . . , b n b_0,...,b_n b 0 , . . . , b n
b n ( t ) = b 0 n ( t ) = ∑ j = 0 n b j ( n i ) t i ( 1 − t ) n − i b^n(t)=b_0^n(t)=\sum_{j=0}^nb_j\begin{pmatrix}n\\i\end{pmatrix}t^i(1-t)^{n-i}
b n ( t ) = b 0 n ( t ) = j = 0 ∑ n b j ( n i ) t i ( 1 − t ) n − i
通过定义与参数有关的多项式对控制点进行插值;
上述例子都是二维的,对三维点同样有效;
在贝塞尔曲线阶数较高(控制点较多)的时候,难以精细控制曲线;
考虑对贝塞尔曲线每四个控制点进行逐段定义;
在曲线连接处,保证另外两个控制点关于共用控制点反向、共线且等距即可保证曲线光滑;
C 0 C^0 C 0 a n = b 0 a_n=b_0 a n = b 0
C 1 C^1 C 1 a n = b 0 = 1 2 ( a n − 1 + b 1 ) a_n=b_0=\frac 12(a_{n-1}+b_1) a n = b 0 = 2 1 ( a n − 1 + b 1 )
C 2 C^2 C 2
相比于贝塞尔曲线,B-样条曲线具有局部性;
B样条与非均匀有理B-样条(NURBS)暂不赘述;
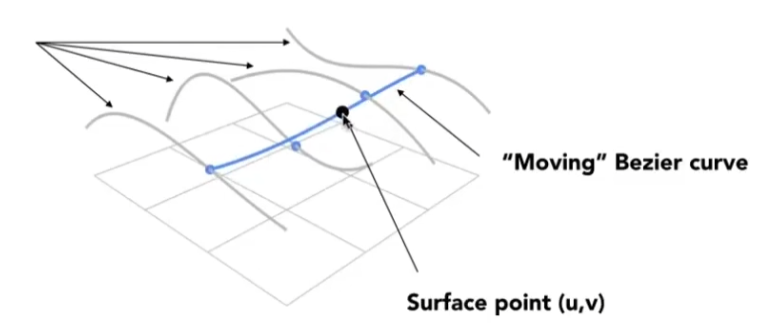
绘制过程可以认为是在两个方向上先后进行贝塞尔曲线绘制;
对网格进行加面,使其更光滑;
Loop 细分(Loop 为人名,与循环无关)的三角形网格细分过程;
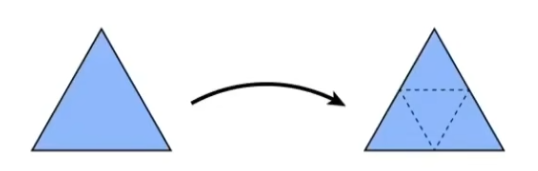
将三角形数量增多;连接三角形三边中点使三角形一分为四;
调整三角形位置;
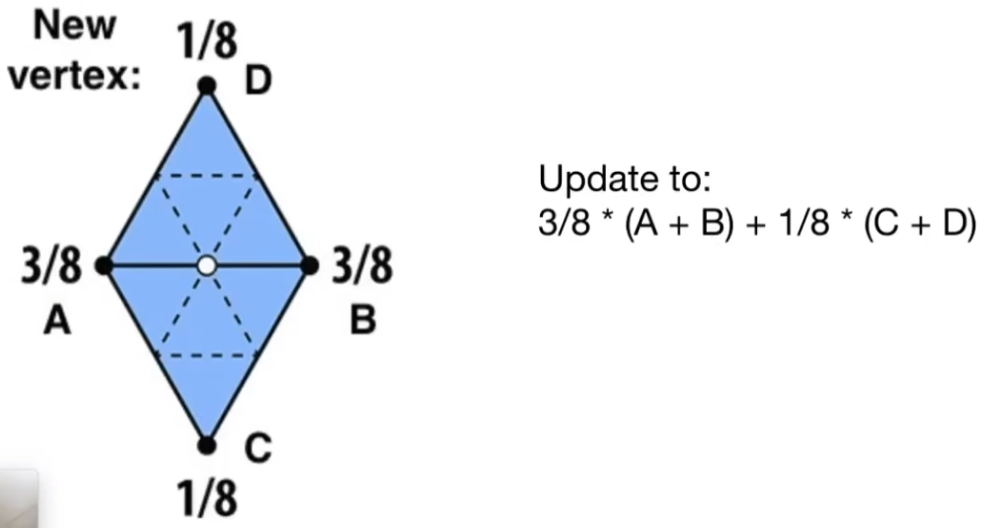
对于新顶点(边中点):
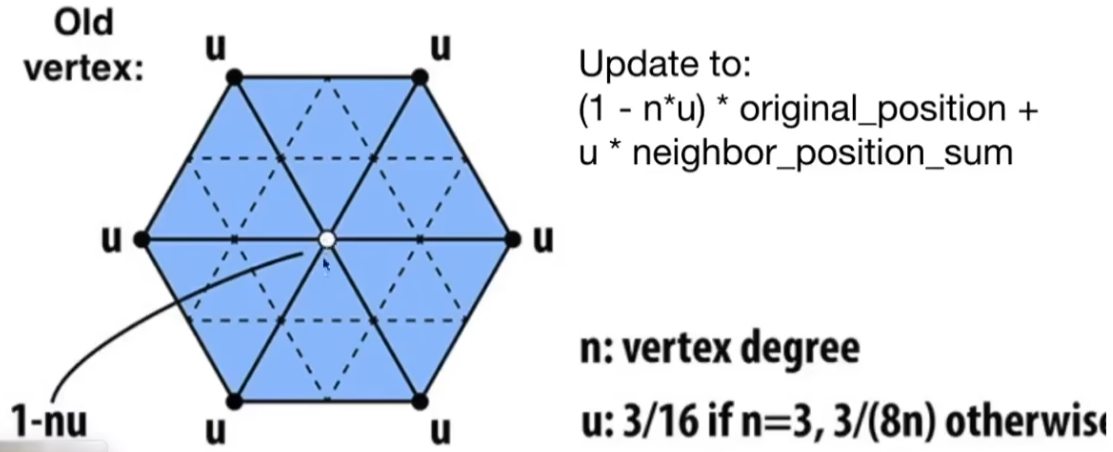
对于旧顶点:
对于一般情况(不全为三角形)可以使用此种方法;
首先将面定义为四边形面(quad face)和非四边形面(non-quad face),将度(相连边数)不为4的点定义为奇异点(extraordinary vertex);
对于每个面取点、边取中点,将面上点和其边中点相连(面取点策略可以取其重心);
在取点连线后,新奇异点数=旧奇异点数+旧非四边形面数,所有旧非四边形面不再存在;也就是说,只有第一次Catmull-Clark细分会增加奇异点数;
接下来进行对点位置的更新;
对于面上点:
对于边上点:
对于旧非奇异点:
对于奇异点的位置更新课程没说,网络资料没有具体说明,猜测可以由3.的公式推广;
在损失可接受的范围内对网格进行简化,节省时空负担;
简单来说即为以点代边,将与边相邻的两个三角形网格坍缩掉,与边相连的其他边汇聚到一个顶点上;
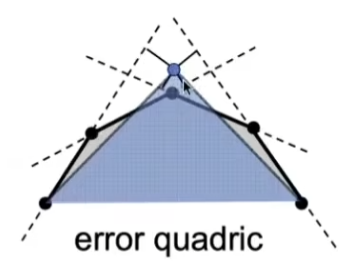
坍缩边后点的位置需要通过二次误差度量(Quadric Error Metrics)得到;
二次误差度量即为将点放在与相关平面距离平方和最小的位置上;
可以选择二次度量误差最小的边来进行坍缩;
坍缩后会影响其他边的二次度量误差,需要更新受影响边的二次度量误差;
消除掉过于长的三角形,使得三角形趋近于正三角形;
光线追踪的不同于光栅化的一种成像方式,解决了光栅化对全局效果的问题(软阴影、Glossy 反射(金属反射)、间接光照);光栅化可以认为是一种快速的、近似的成像方式;
光线可以有如下假设:
在均匀介质中直线传播,不考虑波动性;
光线间不考虑碰撞;
光线从光源发出,最终进入相机;也可以认为从相机发出光线,反向传播最终进入光源(光路可逆);
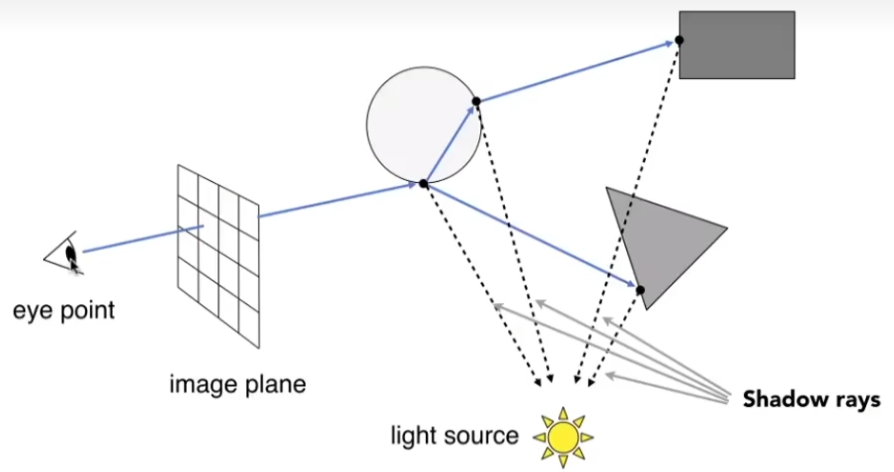
从相机出发,针对每个像素发出一条感知光线(camera ray / primary ray),直至与其相交的第一个三角面;在这个交点上判断对光源的可见性(阴影)(shadow ray),并考虑在此处发生的反射(和折射);沿反射方向继续发出感知光线(secondary ray),重复此过程;
在这个过程中,需要考虑求交、能量损失等若干技术问题;
光线认为是从起点 O ,向方向 d 传播的射线,有参数表示 r ( t ) = o + t d , ( 0 ⩽ t < ∞ ) r(t)=o+td,(0\leqslant t<∞) r ( t ) = o + t d , ( 0 ⩽ t < ∞ )
c 为球心,半径 R 的球有定义 p : ( p − c ) 2 − R 2 = 0 p:(p-c)^2-R^2=0 p : ( p − c ) 2 − R 2 = 0
与光线参数表示联立有
( o + t d − c ) 2 − R 2 = 0 (o+td-c)^2-R^2=0
( o + t d − c ) 2 − R 2 = 0
只有 t 为未知量,解得
a = d ⋅ d b = 2 ( o − c ) ⋅ d c = ( o − c ) ⋅ ( o − c ) − R 2 t = − b ± b 2 − 4 a c 2 a , t ∈ R , t ⩾ 0 a=d\cdot d\\
b=2(o-c)\cdot d\\
c=(o-c)\cdot(o-c)-R^2\\
t={-b \pm \sqrt{b^2-4ac}\over 2a},t\in\R,t\geqslant0
a = d ⋅ d b = 2 ( o − c ) ⋅ d c = ( o − c ) ⋅ ( o − c ) − R 2 t = 2 a − b ± b 2 − 4 a c , t ∈ R , t ⩾ 0
隐式表面有定义 p : f ( p ) = 0 p:f(p)=0 p : f ( p ) = 0
光线参数表示代入有 f ( o + t d ) = 0 f(o+td)=0 f ( o + t d ) = 0
解出正实根即可;
平面可以由法线 N 和平面上一点 p’ 定义,定义有 p : ( p − p ′ ) ⋅ N = 0 p:(p-p')\cdot N=0 p : ( p − p ′ ) ⋅ N = 0
联立有
( o + t d − p ′ ) ⋅ N = 0 t = ( p ′ − o ) ⋅ N d ⋅ N (o+td-p')\cdot N=0\\
t={(p'-o)\cdot N \over d\cdot N}
( o + t d − p ′ ) ⋅ N = 0 t = d ⋅ N ( p ′ − o ) ⋅ N
解出正实根即可;
轴向平面只需要用与其垂直的坐标轴的坐标值即可定义;
以与 x 轴垂直的平面为例,有
t = p x ′ − o x d x t={p'_x-o_x\over d_x}
t = d x p x ′ − o x
比一般平面计算速度更快;
光线与三角形的交点还可以判断光源是否在物体内;
先判断光线和三角形所在平面求交,再判断点是否在三角形内;也可以通过重心坐标直接得到(Möller Trumbore Algorithm);
对于方程
O + t D = ( 1 − b 1 − b 2 ) P 0 + b 1 P 1 + b 2 P 2 O+tD=(1-b_1-b_2)P_0+b_1P_1+b_2P_2
O + t D = ( 1 − b 1 − b 2 ) P 0 + b 1 P 1 + b 2 P 2
定义
E 1 = P 1 − P 0 E 2 = P 2 − P 0 S = O − P 0 S 1 = D × E 2 S 2 = S × E 1 E_1=P_1-P_0\\
E_2=P_2-P_0\\
S=O-P_0\\
S_1=D\times E_2\\
S_2=S\times E_1\\
E 1 = P 1 − P 0 E 2 = P 2 − P 0 S = O − P 0 S 1 = D × E 2 S 2 = S × E 1
有解
[ t b 1 b 2 ] = 1 S 1 ⋅ E 1 [ S 2 ⋅ E 2 S 1 ⋅ S S 2 ⋅ D ] \begin{bmatrix}
t\\
b_1\\
b_2
\end{bmatrix}
=
{\frac 1{S_1\cdot E_1}}
\begin{bmatrix}
S_2\cdot E_2\\
S_1\cdot S\\
S_2\cdot D
\end{bmatrix}
⎣ ⎡ t b 1 b 2 ⎦ ⎤ = S 1 ⋅ E 1 1 ⎣ ⎡ S 2 ⋅ E 2 S 1 ⋅ S S 2 ⋅ D ⎦ ⎤
(上述大写字母均为三位列向量)
如果 t , b 1 , b 2 , 1 − b 1 − b 2 ⩾ 0 t,b_1,b_2,1-b_1-b_2\geqslant0 t , b 1 , b 2 , 1 − b 1 − b 2 ⩾ 0
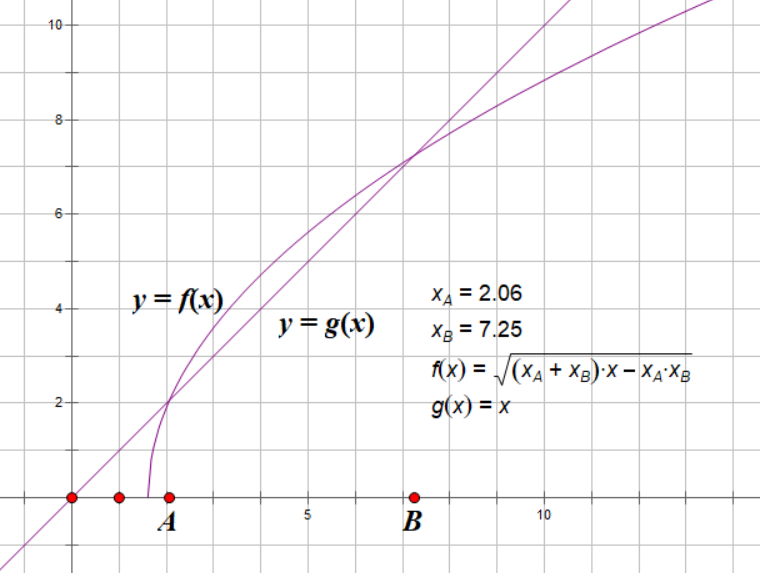
对于光线和一个模型(场景)求交,朴素想法即为枚举面片进行计算,取 t 最小非负值,此种方法消耗很大,考虑加速这一过程;
加速结构的建立是在光线追踪之前;
用简单集合体将模型包围,如果一个光线与包围盒没有交,那么其与包围盒内物体也没有交;
对于轴向对齐包围盒(AABB),可以认为其是三对平面所夹的空间;
考虑光线和包围盒求交过程;当光线与三组对面中的任何一个面均有交点时,认为光线进入包围盒,当光线穿过任何一个对面中的两个平面时,认为光线离开包围盒;
对于每一对面,分别计算 t m i n , t m a x t_{min},t_{max} t m i n , t m a x t e n t e r = max { t m i n } t_{enter}=\max\{t_{min}\} t e n t e r = max { t m i n } t e x i t = min { t m a x } t_{exit}=\min\{t_{max}\} t e x i t = min { t m a x }
如果 t e x i t < 0 t_{exit}<0 t e x i t < 0
如果 t e x i t ⩾ 0 , t e n t e r < 0 t_{exit}\geqslant0,t_{enter}<0 t e x i t ⩾ 0 , t e n t e r < 0
总地来说,如果 t e n t e r < t e x i t , t e x i t ⩾ 0 t_{enter}<t_{exit},t_{exit}\geqslant0 t e n t e r < t e x i t , t e x i t ⩾ 0
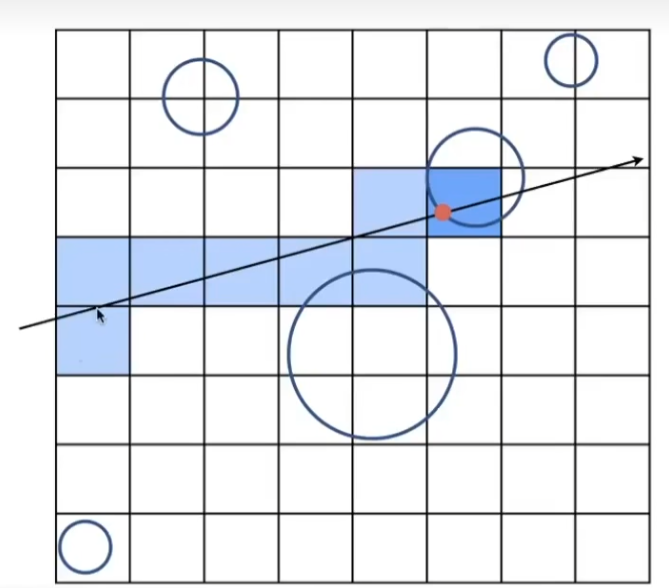
对场景求出包围盒后,将包围盒分为若干均等的小格子,对于包含物体表面的格子进行标记;
沿射线轨迹便理网格,对于遍历到的每个格子,测试射线与格子内对象的相交性,如果相交即停止,意味着找到了第一个交点。
格子划分密度上有经验 # c e l l s = C ∗ # o b j s , C ≈ 27 in 3D \#cells = C * \#objs, C\approx27\text{ in 3D} # c e l l s = C ∗ # o b j s , C ≈ 2 7 in 3D
在几何体分布较为均匀的场景优化效果较好;否则容易出现“‘Teapot in a stadium’ problem”;
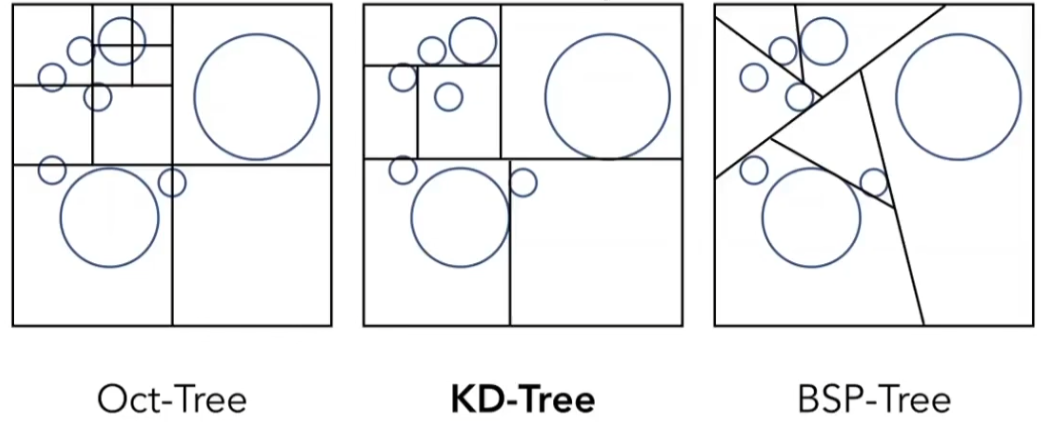
以 KD-Tree 为例详细说明;
对空间进行轴向划分,将每个节点进行八分割存储在子结点中,划分至子结点中有足够少的物体;
不同于八叉树,每次只对节点进行一次轴向划分,不对于父子节点进行相同轴向的划分(三维上沿 x ,y ,z 方向上循环),同样直至子结点中有足够少的物体;
只需要在叶子节点存储模型;
在判断时,先判断与根节点是否存在交点,如果有交点则判断与两子节点是否存在交点;直至叶子节点,如果仍有交点则判断其与节点内部模型是否有交点;
KD-Tree 的主要问题是难以判断格点与哪些模型相交;此外,如果一个物体与多个叶子节点相交,其会被存储多份;
不同于KD-Tree进行轴向划分,对节点进行更自由的二分;
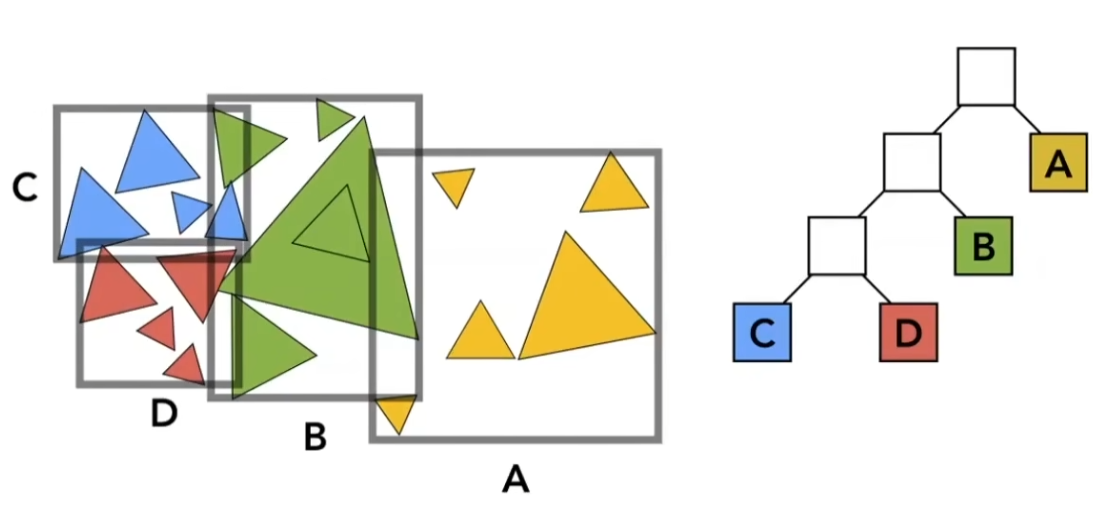
BVH树对物体进行划分,如图所示,直至划分至子结点中有足够少的三角形;
BVH树解决了 KD-Tree 的两大问题;
其存在的问题是节点包围盒可能相交,影响有限;实际上会保证重叠部分尽量少;
关于如何划分节点:
类似 KD-Tree ,可以循环使用不同的轴向;也可以选择包围盒最长的一条轴进行划分;
对于如何划分两半,可以将三角形的重心按分割轴向排序,取中位三角形进行分隔,使得两部分三角形数量均匀,降低资源消耗;
寻找中位数不需要排序,可以转化为top-k大数问题,通过快速选择算法在线性复杂度内解决;
在场景变化时,需要重新计算BVH树;
与 KD-Tree 类似,在中间节点只存储包围盒和子节点指针,只在叶子节点存储分割后的模型;
光线求交过程也与 KD-Tree 类似,有伪代码
1 2 3 4 5 6 7 8 9 10 11 12 13 Intersect (Ray ray, BVH node) {if (ray misses node.bbox) return ;if (node is a leaf node)return closest intersection;Intersect (ray, node.child1);Intersect (ray, node.child2);return the closer of hit1, hit2;
辐射度量学是一种精确定义光与物体表面作用的工具,是路径追踪的基础;
辐射度量学同样着眼于光的几何属性,忽略波动性;
辐射度量学通过辐射通量(Radiant flux)、强度(Intensity)、照度(Intensity)、亮度(Radiance)等属性描述光,下述均使用英文;
Radiant Energy 是电磁辐射的能量,以焦耳(J)表示;
Q [ J=Joule ] Q[\text{J=Joule}]
Q [ J=Joule ]
Radiant Flux 是电磁辐射的功率,单位时间的能量,也可以被度量为单位时间内辐射出的光子数量,以瓦特(W)或流明(lm)表示;
Φ = d Φ d t [ W=Watt ] [ lm=lumen ] \Phi =\frac {\mathrm{d}\Phi}{\mathrm{d}t}[\text{W=Watt}][\text{lm=lumen}]
Φ = d t d Φ [ W=Watt ] [ lm=lumen ]
现代11W LED灯约815lm,等价于60W白炽灯;
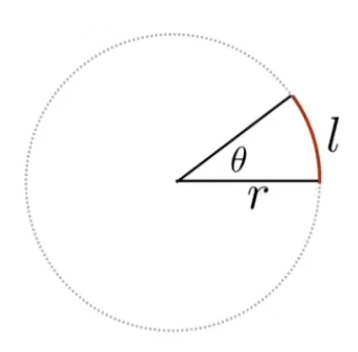
类比于角度 θ = l r \theta =\frac lr θ = r l 2 π 2\pi 2 π
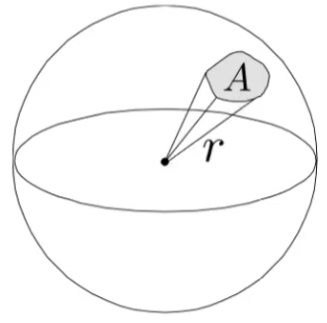
立体角是角度的三维延伸,Ω = A r 2 \Omega=\frac A{r^2} Ω = r 2 A 4 π 4\pi 4 π
(Radiant) Intensity 是对光源方向上功率的度量,每单位立体角的功率,以坎德拉(cd)表示;
I ( ω ) = d Φ d ω [ W sr ] [ lm sr =cd=candela ] I(\omega) =\frac {\mathrm{d}\Phi}{\mathrm{d}\omega}[\frac {\text{W}}{\text{sr}}][\frac {\text{lm}}{\text{sr}}\text{=cd=candela}]
I ( ω ) = d ω d Φ [ sr W ] [ sr lm =cd=candela ]
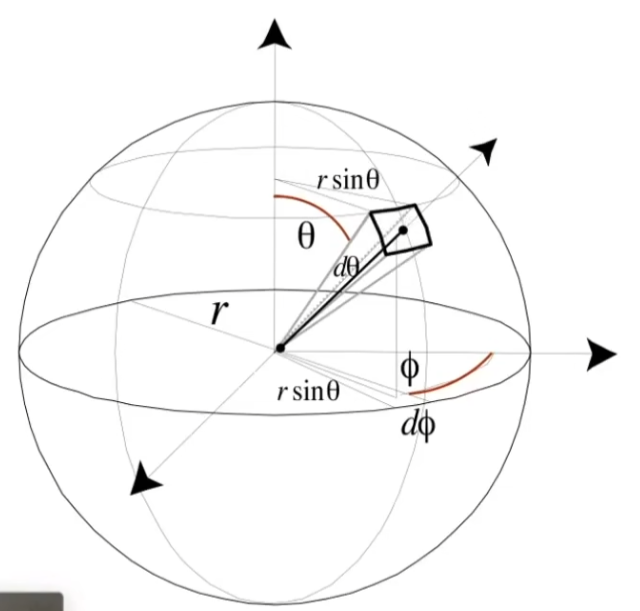
单位立体角可以由天顶角 θ \theta θ ϕ \phi ϕ
d A = ( r d θ ) ( r sin θ d ϕ ) = r 2 sin θ d θ d ϕ d ω = d A r 2 = sin θ d θ d ϕ I = Φ 4 π \mathrm{d}A=(r\mathrm{d}\theta)(r\sin\theta\mathrm{d}\phi)\\
=r^2\sin\theta\text{ }\mathrm{d}\theta\mathrm{d}\phi\\
\mathrm{d}\omega=\frac{\mathrm{d}A}{r^2}=\sin\theta\text{ }\mathrm{d}\theta\mathrm{d}\phi\\
I=\frac {\Phi}{4\pi}
d A = ( r d θ ) ( r sin θ d ϕ ) = r 2 sin θ d θ d ϕ d ω = r 2 d A = sin θ d θ d ϕ I = 4 π Φ
ω \omega ω
Irradiance 是对物体表面单位面积接收到光的功率的度量;
E ( x ) ≡ d Φ ( x ) d A [ W m 2 ] [ l m m 2 = lux ] E(x)\equiv\frac{\mathrm{d}\Phi(x)}{\mathrm{d}A}[\frac W{m^2}][\frac{lm}{m^2}=\text{lux}]
E ( x ) ≡ d A d Φ ( x ) [ m 2 W ] [ m 2 l m = lux ]
要求单位平面与光线垂直;
Radiance 是对光线传播中的度量,是每单位立体角单位面积上的功率;
L ( p , ω ) ≡ d 2 Φ ( p , ω ) d ω d A cos θ [ W sr m 2 ] [ cd m 2 = lm sr m 2 = nit ] L(p,\omega)\equiv\frac{\mathrm{d^2}\Phi(p,\omega)}{\mathrm{d}\omega\mathrm{d}A\cos\theta}
[\frac {\text{W}}{\text{sr }\text{m}^2}][\frac {\text{cd}}{\text{m}^2}=\frac {\text{lm}}{\text{sr }\text{m}^2}=\text{nit}]
L ( p , ω ) ≡ d ω d A cos θ d 2 Φ ( p , ω ) [ sr m 2 W ] [ m 2 cd = sr m 2 lm = nit ]
d A cos θ \mathrm{d}A\cos\theta d A cos θ
联系前面的两个量,有
L ( p , ω ) = d E ( p ) d ω cos θ L ( p , ω ) = d I ( p , ω ) d A cos θ L(p,\omega)=\frac{\mathrm{d}E(p)}{\mathrm{d}\omega\cos\theta}\\
L(p,\omega)=\frac{\mathrm{d}I(p,\omega)}{\mathrm{d}A\cos\theta}
L ( p , ω ) = d ω cos θ d E ( p ) L ( p , ω ) = d A cos θ d I ( p , ω )
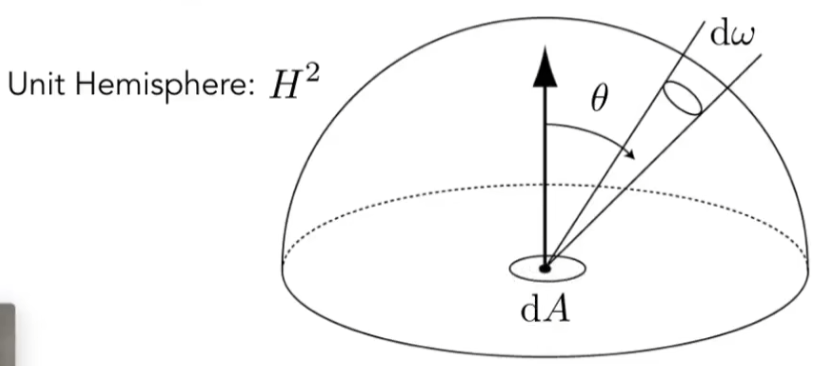
图形学上常用物理量为 Irradiance 和 Radiance ,Irradiance可以理解为单位面积吸收的总能量,Radiance 为单位面积从 d ω \mathrm{d}\omega d ω
d E ( p , ω ) = L i ( p , ω ) cos θ d ω E ( p ) = ∫ H 2 L i ( p , ω ) cos θ d ω \mathrm{d}E(p,\omega)=L_i(p,\omega)\cos\theta\mathrm{d}\omega\\
E(p)=\int_{H^2}L_i(p,\omega)\cos\theta\mathrm{d}\omega
d E ( p , ω ) = L i ( p , ω ) cos θ d ω E ( p ) = ∫ H 2 L i ( p , ω ) cos θ d ω
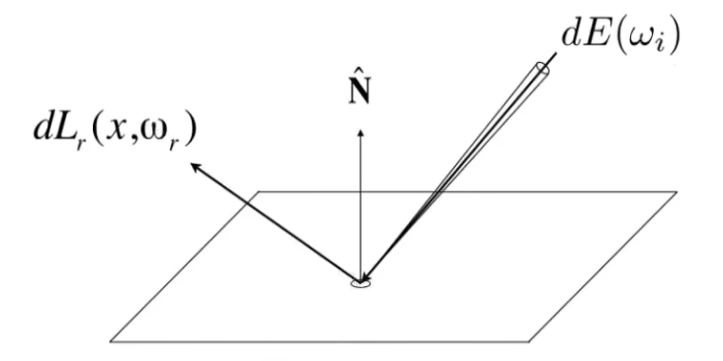
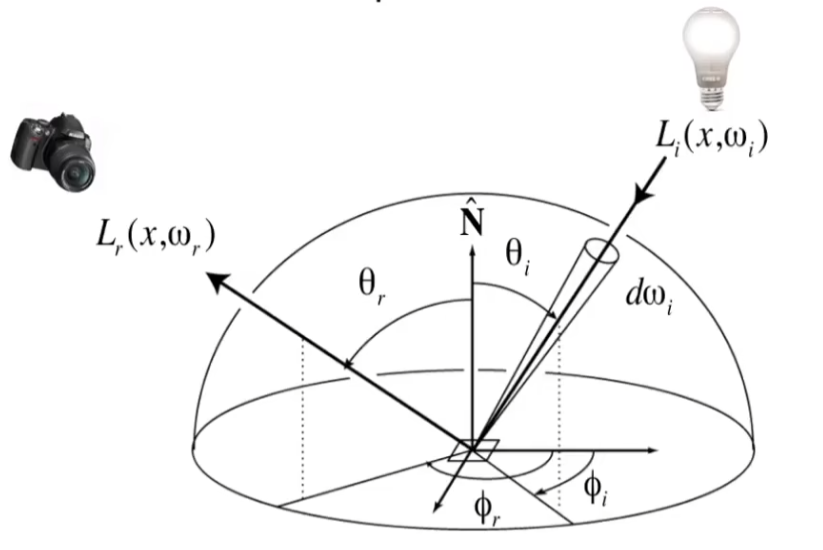
反射可以认为是从方向 ω i \omega_i ω i d A \mathrm{d}A d A E E E ω r \omega_r ω r
BRDF描述了各个其他方向 ω r \omega_r ω r
f r ( ω i → ω r ) = d L r ( ω r ) d E i ( ω i ) = d L r ( ω r ) L i ( ω i ) cos θ i d ω i [ 1 sr ] f_r(\omega_i\to\omega_r)={\mathrm{d}L_r(\omega_r)\over\mathrm{d}E_i(\omega_i)}={\mathrm{d}L_r(\omega_r)\over L_i(\omega_i)\cos\theta_i\mathrm{d}\omega_i}[\frac 1{\text{sr}}]
f r ( ω i → ω r ) = d E i ( ω i ) d L r ( ω r ) = L i ( ω i ) cos θ i d ω i d L r ( ω r ) [ sr 1 ]
那么某方向接收到的反射光即为
L r ( p , ω r ) = ∫ H 2 f r ( p , ω i → ω r ) L i ( p , ω i ) cos θ i d ω i L_r(p,\omega_r)=\int_{H^2}f_r(p,\omega_i\to\omega_r)L_i(p,\omega_i)\cos\theta_i\mathrm{d}\omega_i
L r ( p , ω r ) = ∫ H 2 f r ( p , ω i → ω r ) L i ( p , ω i ) cos θ i d ω i
如果物体自发光,那么就有了渲染方程
L o ( p , ω o ) = L e ( p , ω o ) + ∫ Ω + f r ( p , ω i , ω o ) L i ( p , ω i ) ( n ⋅ ω i ) d ω i L_o(p,\omega_o)=L_e(p,\omega_o)+\int_{\Omega^+}f_r(p,\omega_i,\omega_o)L_i(p,\omega_i)(n\cdot\omega_i)\mathrm{d}\omega_i
L o ( p , ω o ) = L e ( p , ω o ) + ∫ Ω + f r ( p , ω i , ω o ) L i ( p , ω i ) ( n ⋅ ω i ) d ω i
L e L_e L e ω i \omega_i ω i
记 E 为自发光,K为反射操作符,L 可以记为 L = E + K E + K 2 E + . . . L=E+KE+K^2E+... L = E + K E + K 2 E + . . .
计算难以解析求解的函数定积分的一种数值方法;
若求定积分 ∫ a b f ( x ) d x \int_a^bf(x)\mathrm{d}x ∫ a b f ( x ) d x X i ∼ p ( x ) X_i\sim p(x) X i ∼ p ( x ) F N = 1 N ∑ i = 1 N f ( X i ) p ( X i ) F_N=\frac 1N\sum_{i=1}^N\frac{f(X_i)}{p(X_i)} F N = N 1 ∑ i = 1 N p ( X i ) f ( X i ) ∫ a b p ( x ) d x = 1 \int_a^bp(x)\mathrm{d}x=1 ∫ a b p ( x ) d x = 1
如果随机变量均匀分布,则结果有 F N = b − a N ∑ i = 1 N f ( X i ) F_N=\frac {b-a}N\sum_{i=1}^Nf(X_i) F N = N b − a ∑ i = 1 N f ( X i )
N 越大,结果越准确;
在 p(x) 与 f(x) 形状一致时,误差最小;
Whitted风格光线追踪总是进行镜面反射 / 折射,停止在漫反射表面,存在难以处理金属反射(glossy reflection)质感、无漫反射等问题;
对于渲染方程,我们需要递归地通过蒙特卡洛解半球上的积分;
我们的概率密度函数可以取 p ( ω i ) = 1 2 π p(\omega_i)=\frac 1 {2\pi} p ( ω i ) = 2 π 1
L o ( p , ω o ) ≈ L e ( p , ω o ) + 2 π N ∑ i = 1 N f r ( p , ω i , ω o ) L i ( p , ω i ) ( n ⋅ ω i ) L_o(p,\omega_o)\approx L_e(p,\omega_o)+\frac {2\pi}N\sum_{i=1}^N{f_r(p,\omega_i,\omega_o)L_i(p,\omega_i)(n\cdot\omega_i)}
L o ( p , ω o ) ≈ L e ( p , ω o ) + N 2 π i = 1 ∑ N f r ( p , ω i , ω o ) L i ( p , ω i ) ( n ⋅ ω i )
1 2 3 4 5 6 7 8 9 10 shade (p,wo) 0.0 r (p, wi)2 * pi / N ) * L_i * f_r * cosine2 * pi / N ) * shade (q, -wi) * f_r * cosine
上面的伪代码复杂度不可接受,若使 N=1 则有
1 2 3 4 5 6 7 8 shade (p,wo) 1 direction wi~PDF0.0 r (p, wi)Return ( 2 * pi ) * L_i * f_r * cosineReturn ( 2 * pi ) * shade (q, -wi) * f_r * cosine
N!=1 时即为分布式光线追踪(Distributed Ray Tracing),现很少使用;
对于降低 N 造成的偏差,我们可以通过对于一个像素多次进行路径追踪并平均结果得到;
对于射线生成(Ray Generation),有伪代码
1 2 3 4 5 6 7 8 ray_generation (camPos,pixel)0.0 r (camPos, cam_to_sample)1 / N * shade (p, sample_to_cam)
上述 shade 代码依然存在递归终止条件的问题,我们选择轮盘赌策略(Russian Roulette,RR),在满足一定条件时停止递归;
如果有一个概率 P ,我们有 P 的概率发出光线,对于得到的 L o L_o L o L o / P L_o/P L o / P L o L_o L o
1 2 3 4 5 6 7 8 9 10 11 12 shade (p,wo) 0 , 1 ]If (ksi > P_RR) return 0.0 1 direction wi~PDF0.0 r (p, wi)Return ( 2 * pi ) * L_i * f_r * cosine / P_RRReturn ( 2 * pi ) * shade (q, -wi) * f_r * cosine / P_RR
也可以通过控制 P_RR 来控制期望弹射次数(递归深度)为 1/(1-P_RR) ;
此时即为路径追踪;
在低 SPP(samples per pixel)时,生成速度更快但会产生噪点;下面考虑加速;
如果光源很小,那么采样线打到光源的概率很低,浪费了很多的计算能力;
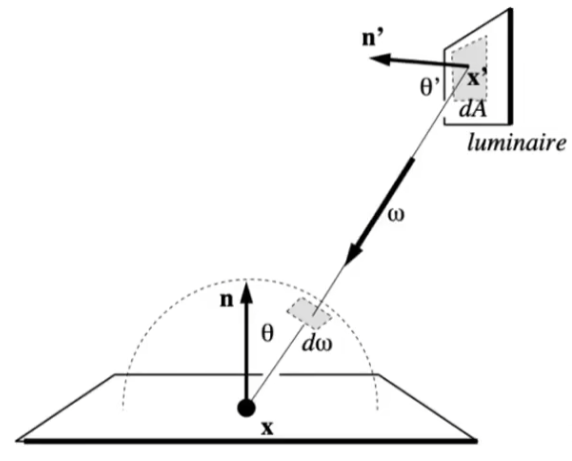
我们考虑对光源采样,将积分从 d ω \mathrm{d}\omega d ω d A \mathrm{d}A d A
有关系
d ω = d A cos θ ′ ∣ ∣ x ′ − x ∣ ∣ 2 \mathrm{d}\omega =\frac{\mathrm{d}A\cos\theta'}{||x'-x||^2}
d ω = ∣ ∣ x ′ − x ∣ ∣ 2 d A cos θ ′
渲染方程换元有
L o ( p , ω o ) = L e ( p , ω o ) + ∫ A f r ( p , ω i , ω o ) L i ( p , ω i ) cos θ cos θ ′ ∣ ∣ x ′ − p ∣ ∣ 2 d A L_o(p,\omega_o)=L_e(p,\omega_o)+\int_{A}f_r(p,\omega_i,\omega_o)L_i(p,\omega_i)\frac{\cos\theta\cos\theta'}{||x'-p||^2}\mathrm{d}A
L o ( p , ω o ) = L e ( p , ω o ) + ∫ A f r ( p , ω i , ω o ) L i ( p , ω i ) ∣ ∣ x ′ − p ∣ ∣ 2 cos θ cos θ ′ d A
考虑着色点的贡献来自于所有的光源和非光源,来自于光源的部分不需要 RR 策略来加速,来自于非光源的部分采用前述方法;
有伪代码
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 shade(p, wo)the light at x' ( pdf_light = 1 / A)from p to x'the ray is not blocked in the middle 2 / pdf_light0.0 with probability P_RRthe hemisphere toward wi (pdf_hemi = 1 / 2 pi )at q return L_dir + L_indir
对于点光源的处理比较困难,课程内暂不赘述;
事实上计算出的 radiance 并不是颜色,需要进行伽马矫正(gamma correction);
对材质的定义等价于对 BRDF 的定义;
对于漫反射模型,假设入射光被均匀地反射到半球上的各个方向(f r f_r f r
L o ( ω o ) = ∫ H 2 f r L i ( ω i ) cos θ i d ω i = f r L i ∫ H 2 cos θ i d ω i = π f r L i L_o(\omega_o)=\int_{H^2}f_rL_i(\omega_i)\cos\theta_i\mathrm{d}\omega_i\\
=f_rL_i\int_{H^2}\cos\theta_i\mathrm{d}\omega_i\\
=\pi f_rL_i
L o ( ω o ) = ∫ H 2 f r L i ( ω i ) cos θ i d ω i = f r L i ∫ H 2 cos θ i d ω i = π f r L i
在能量守恒的假设下,有 f r = 1 π f_r=\frac 1 \pi f r = π 1 ρ ∈ [ 0 , 1 ] \rho\in[0,1] ρ ∈ [ 0 , 1 ] f r = ρ π f_r=\frac \rho\pi f r = π ρ
对于不同金属,金属反射性质也不同;
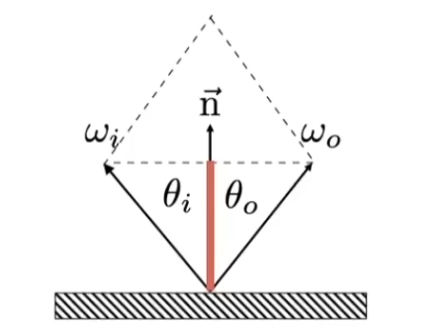
由出射角等于入射角,有
ω o + ω i = 2 cos θ n ⃗ = 2 ( ω i ⋅ n ⃗ ) n ⃗ w o = − w i + 2 ( ω i ⋅ n ⃗ ) n ⃗ \omega_o+\omega_i=2\cos\theta\vec n=2(\omega_i\cdot\vec n)\vec n\\
w_o=-w_i+2(\omega_i\cdot\vec n )\vec n
ω o + ω i = 2 cos θ n = 2 ( ω i ⋅ n ) n w o = − w i + 2 ( ω i ⋅ n ) n
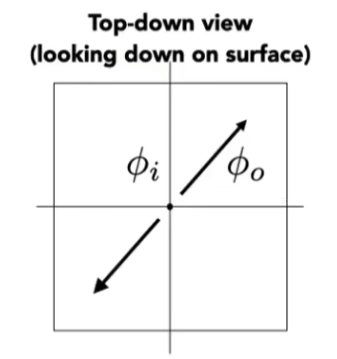
对于方位角,有
ϕ o = ( ϕ i + π ) m o d 2 π \phi_o=(\phi_i+\pi)\mod 2\pi
ϕ o = ( ϕ i + π ) m o d 2 π
镜面反射的 BRDF 值与 delta 函数有关,课程内暂不赘述;
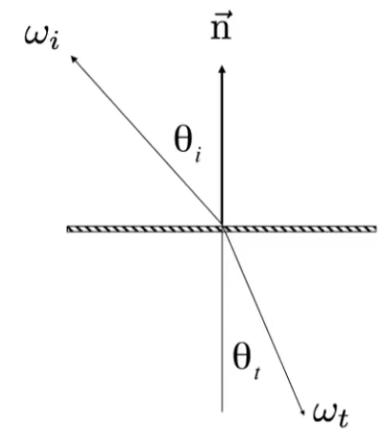
由折射定律(Snell’s Law)得
η i sin θ i = η t sin θ t \eta_i\sin\theta_i=\eta_t\sin\theta_t
η i sin θ i = η t sin θ t
其中 η i , η t \eta_i,\eta_t η i , η t
cos θ t = 1 − ( η i η t ) 2 ( 1 − cos 2 θ i ) \cos\theta_t=\sqrt{1-(\frac {\eta_i} {\eta_t})^2(1-\cos^2\theta_i)}
cos θ t = 1 − ( η t η i ) 2 ( 1 − cos 2 θ i )
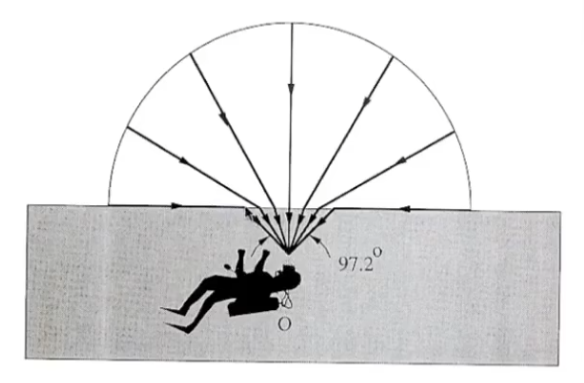
如果 1 − ( η i η t ) 2 ( 1 − cos 2 θ i ) < 0 1-(\frac {\eta_i} {\eta_t})^2(1-\cos^2\theta_i)<0 1 − ( η t η i ) 2 ( 1 − cos 2 θ i ) < 0
其中可视锥体被称为 Snell’s Window ;
方位角同镜面反射;
描述折射性质的函数被称为 BTDF ,与 BRDF 统称为 BSDF ;
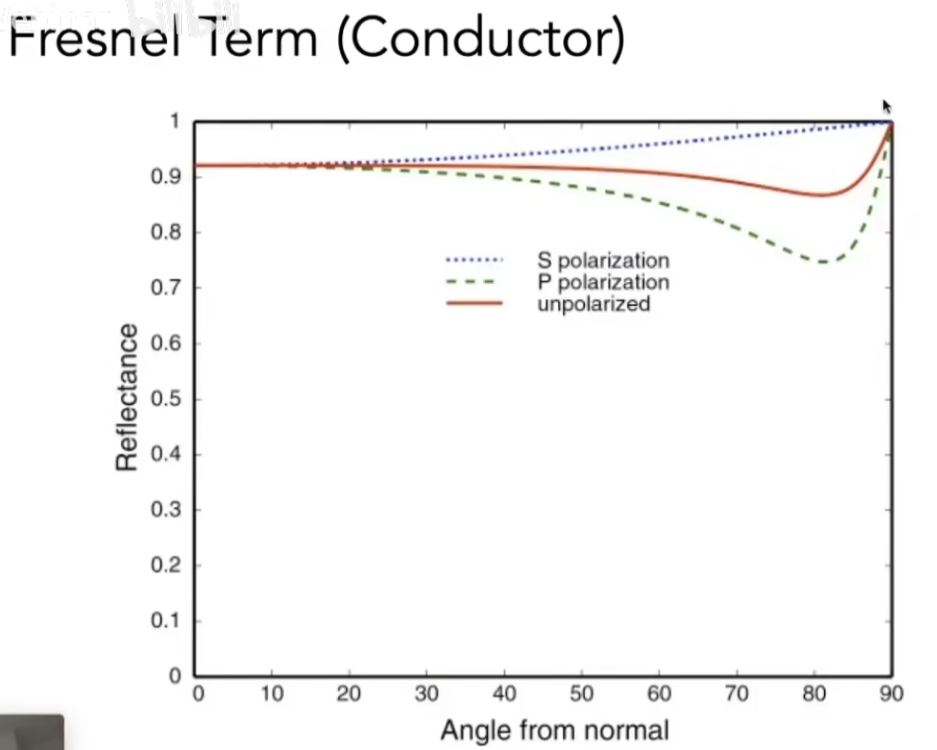
菲涅尔项描述了反射和折射的比例;
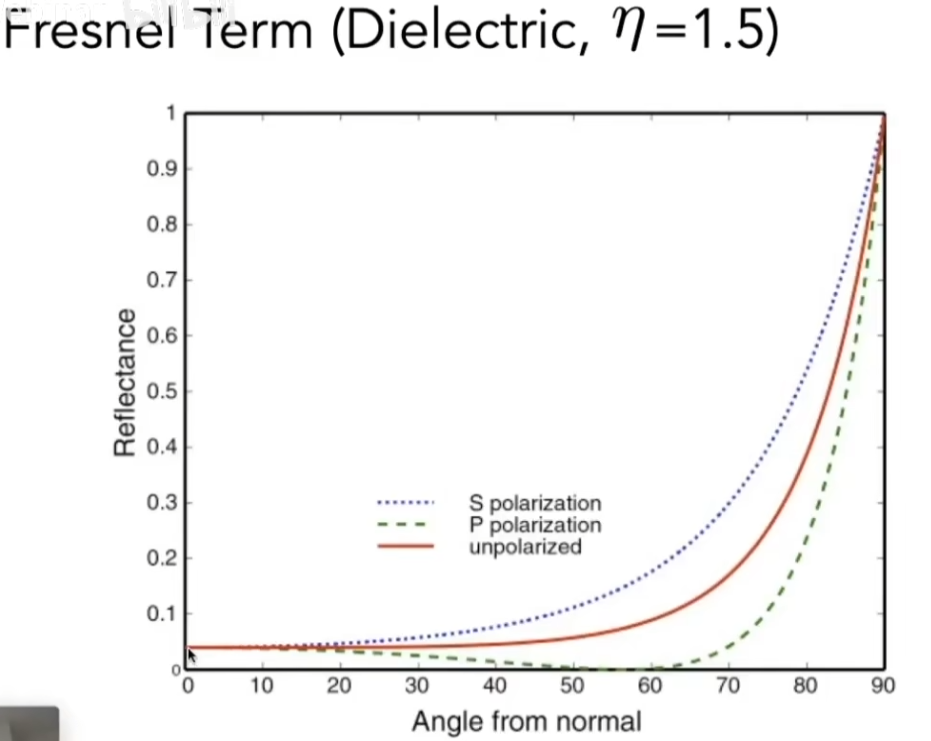
对于绝缘体表面,有
S 和 P 描述了两种偏振光的表现,一般情况性质如红线描述;
对于金属(导体)表面,则有
对于两种偏振光的反射率有(n 1 , n 2 n_1,n_2 n 1 , n 2
对于无偏振的光,有
R e f f = 1 2 ( R s + R p ) R_{eff}=\frac 12 (R_s+R_p)
R e f f = 2 1 ( R s + R p )
由于上述计算比较复杂,有简化公式 Schlick’s approximation :
基准反射率即为法线入射时的反射率,为
R 0 = ( n 1 − n 2 n 1 + n 2 ) 2 R_0=(\frac{n_1-n_2}{n_1+n_2})^2
R 0 = ( n 1 + n 2 n 1 − n 2 ) 2
关于入射角的反射率为
R ( θ ) = R 0 + ( 1 − R 0 ) ( 1 − cos θ ) 5 R(\theta)=R_0+(1-R_0)(1-\cos\theta)^5
R ( θ ) = R 0 + ( 1 − R 0 ) ( 1 − cos θ ) 5
对导体和绝缘体均可以近似;
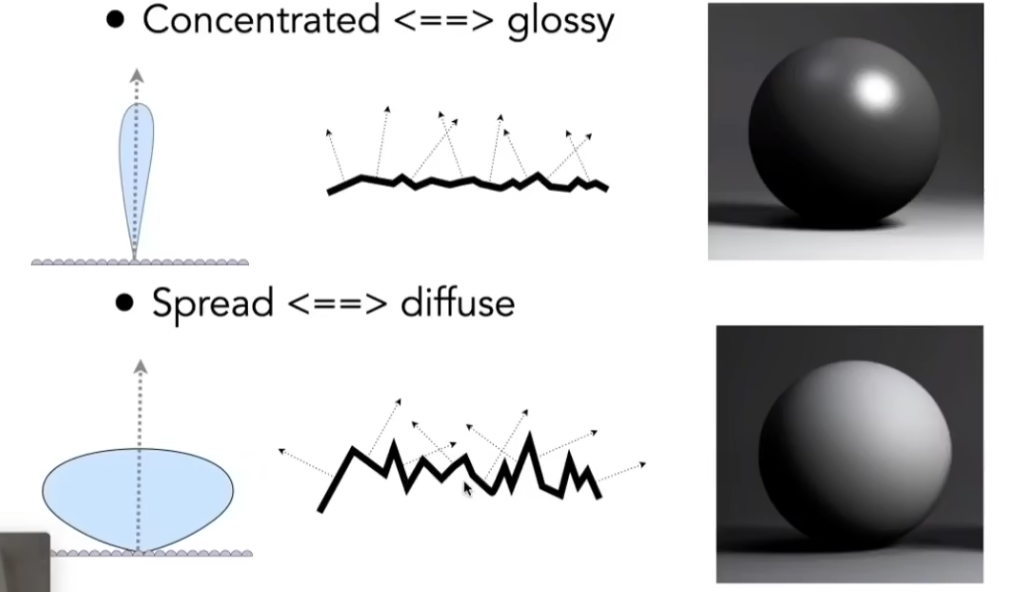
微表面模型假设物体表面是粗糙的,由很多微表面组成,每一个微表面只进行镜面反射,具有自己的法线;远看是外观,近看是几何;
通过描述微表面法线的分布来描述物体粗糙程度,例如
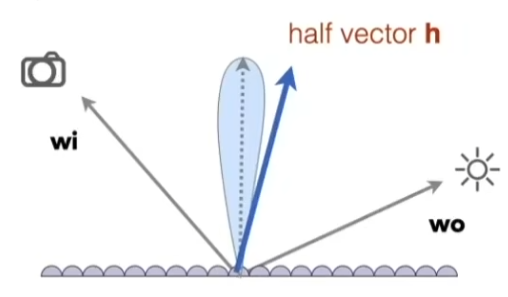
微表面模型的 BRDF 有
f ( i , o ) = F ( i , h ) D ( h ) G ( i , o , h ) 4 ( n , i ) ( n , o ) f(i,o)={F(i,h)D(h)G(i,o,h)\over4(n,i)(n,o)}
f ( i , o ) = 4 ( n , i ) ( n , o ) F ( i , h ) D ( h ) G ( i , o , h )
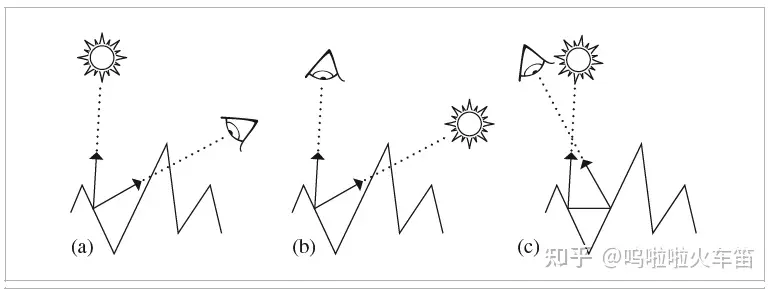
其中 h 为 i 和 o 的中间向量,F 为菲涅尔项,D 为微表面法向的概率密度函数,G 为几何项,定义了了微表面互相遮挡造成的影响;
在入射方向或观察方向和表面几乎平行时(Grazing Angle 掠射角度),表面遮挡比较严重,此时 G 项的值会比较小;
GGX模型下,对于粗糙度为 α \alpha α
D ( n , h , α ) = α 2 π ( ( n ⋅ h ) 2 ( α 2 − 1 ) + 1 ) 2 k = ( α + 1 ) 2 8 G ( i , o , n ) = n ⋅ i ( n ⋅ i ) ( 1 − k ) + k n ⋅ o ( n ⋅ o ) ( 1 − k ) + k D(n,h,\alpha)={\alpha^2\over\pi((n\cdot h)^2(\alpha^2-1)+1)^2}\\
k=\frac{(\alpha+1)^2}8\\
G(i,o,n)={n\cdot i\over(n\cdot i)(1-k)+k}{n\cdot o\over(n\cdot o)(1-k)+k}
D ( n , h , α ) = π ( ( n ⋅ h ) 2 ( α 2 − 1 ) + 1 ) 2 α 2 k = 8 ( α + 1 ) 2 G ( i , o , n ) = ( n ⋅ i ) ( 1 − k ) + k n ⋅ i ( n ⋅ o ) ( 1 − k ) + k n ⋅ o
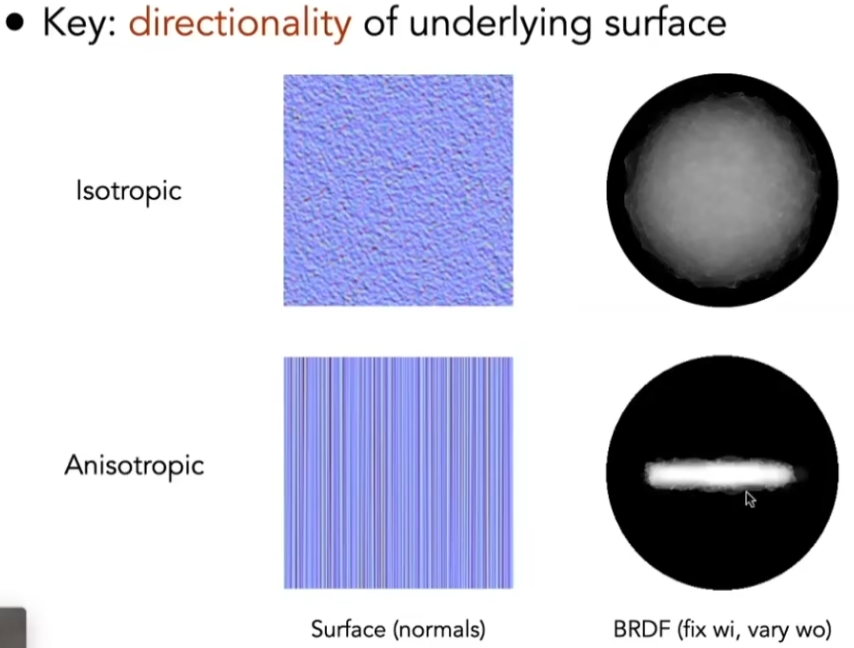
类似于电梯内表面的纵向抛光痕迹,一些材料表面是各向异性的;
各向同性即认为微表面不存在方向性或方向性很弱;
从 BRDF 考虑,高度角固定的情况下,如果对于固定方位角变化量,函数值不同,即为各向异性;
非负:f r ( ω i → ω r ) ⩾ 0 f_r(\omega_i\to\omega_r)\geqslant0 f r ( ω i → ω r ) ⩾ 0
线性;
可逆性:f r ( ω i → ω r ) = f r ( ω r → ω i ) f_r(\omega_i\to\omega_r)=f_r(\omega_r\to\omega_i) f r ( ω i → ω r ) = f r ( ω r → ω i )
能量守恒: ∀ ω r , ∫ H 2 f r ( ω i → ω r ) cos θ i d ω i ⩽ 1 \forall \omega_r,\int_{H^2}f_r(\omega_i\to\omega_r)\cos\theta_i\mathrm{d}\omega_i\leqslant1 ∀ ω r , ∫ H 2 f r ( ω i → ω r ) cos θ i d ω i ⩽ 1
各向同性与各向异性;
gonioreflectometer
MERL BRDF Database 对各向同性材料进行了三个维度的测量 ( θ i , θ o , ∣ ϕ i − ϕ o ∣ ) (\theta_i,\theta_o,|\phi_i-\phi_o|) ( θ i , θ o , ∣ ϕ i − ϕ o ∣ ) 90 ∗ 90 ∗ 180 90*90*180 9 0 ∗ 9 0 ∗ 1 8 0
基于无偏蒙特卡洛算法(无论采用多少样本,期望均等于真实值)的光线追踪即为无偏光线追踪;
对于有偏蒙特卡洛算法,存在一种特殊情况,即为在样本趋近于无穷多时为无偏的,被称为一致的(consistent);
BDPT 利用光向可逆性,从光源和相机分别发出一条半路径,两端点重合时即可成为一条路径;
在相同spp时,双向路径追踪效果更好,能够更有效地找到能量集中的路径;在光线传播集中在光源附近时表现更优;
使用马尔可夫链(Markov Chain Monte Carlo ,MCMC)进行采样,可以基于一个样本生成相近的其他样本;
MLT 对于复杂光路(例如 SDS(Specular-Diffuse-Specular))效果更优,可以基于一条有效光路更快地找到有效的光路;
但是难以估计收敛速度,不能保证每个像素收敛速度相同(会形成不可控的脏点),因此不适合渲染动画;
适合渲染 caustics 现象和复杂光路(例如SDS);
光子映射的一种实现方法:
首先从光源出发模拟光子的运动,直至到达漫反射面;再从相机发出半路径,直至打到漫反射面;对相机出发的半路径终点进行局部密度估计(local density estimation)来计算像素的亮度;
局部密度估计即为对于某个点找周围的最近 n 个光子,结合这 n 个光子所占面积计算局部光子密度,进而计算亮度;
对于 n 更小的取值,结果噪声更多;对于 n 更大的取值,结果更模糊;
有偏体现在
d N / d A ≠ Δ N / Δ A \mathrm{d}N/\mathrm{d}A\not=\Delta N/\Delta A
d N / d A = Δ N / Δ A
结合了双向路径追踪和光子映射的过程;
假设双向路径终点再同一个表面上但是并不重合,就让相机端半路径作为光子进行光子映射;
从光源打出半路径,将已经被照亮的表面当作光源(虚拟点光源,Virtual Point Light ,VPL)处理;
渲染时仅通过直接光照即可;
在接缝处会出现“漏光”,无法处理金属反射;
光线在穿过散射介质时会发生散射;
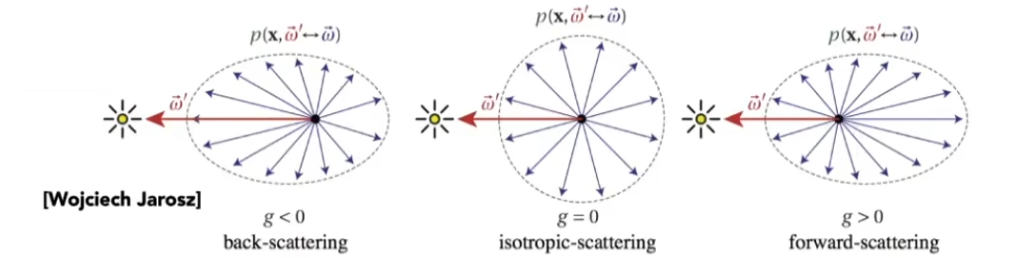
散射可以由相位函数(Phase Function)来定义
在散射云中,每次从上一个着色点随机选择一个方向和一段距离确定下一个着色点,在每一个着色点连接到光源进行着色;
不止云、雾和霾,很多材质都可以视为散射介质,比如说手指和胶体;
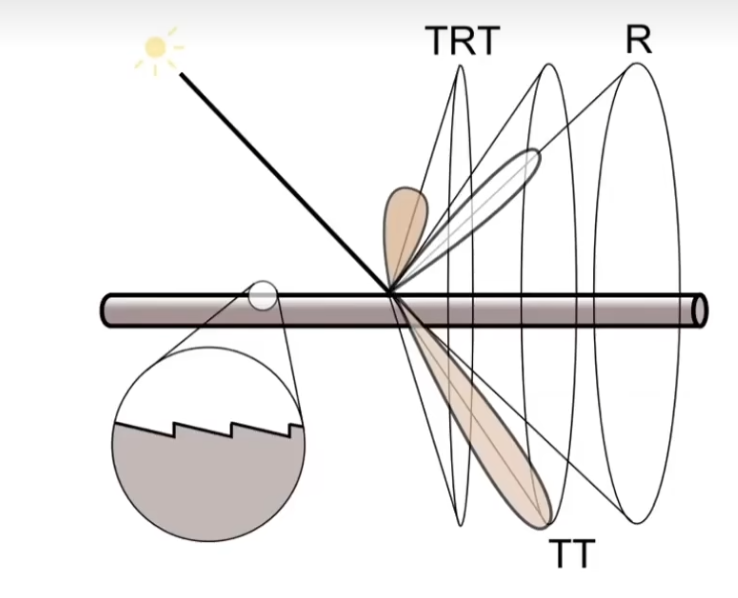
Marschner Model 将头发视为玻璃圆柱,表层和含颜色的填充层;
光线与单根头发的作用分为三个部分,反射(R),穿透(TT),内壁反射(TRT)
T 为 transmission(传递),R 为 reflection ;
通过多次散射达到对于头发表面的渲染;
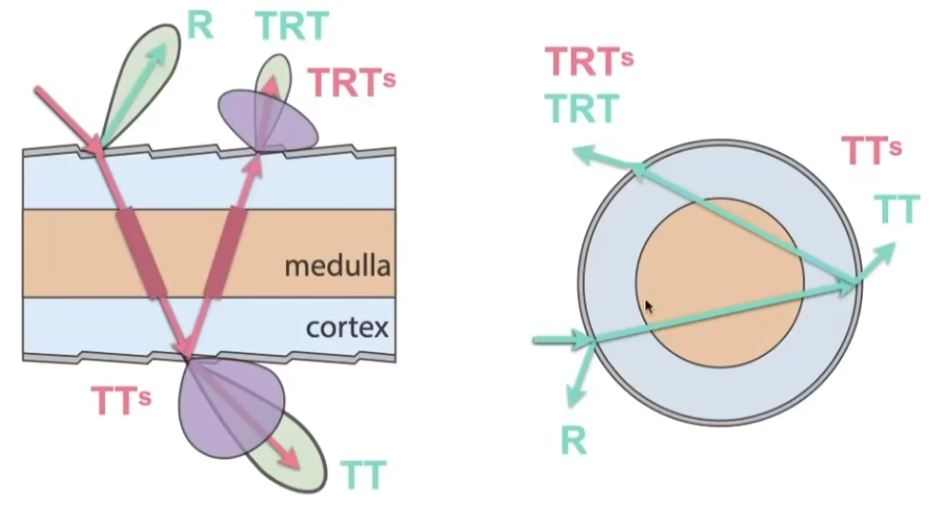
基于毛发在解剖角度上存在髓质,有双圆柱模型,在上述模型的基础上添加了负责反射的髓质芯;此时光线和毛发的作用在上述基础上还增加了“发生散射并穿透(TTs)”和“发生散射并内部反射(TRTs)”;
如盐、糖、沙子;
通过对单元内组分的定义来进行渲染;
过于耗时,没有比较好的解决方案;
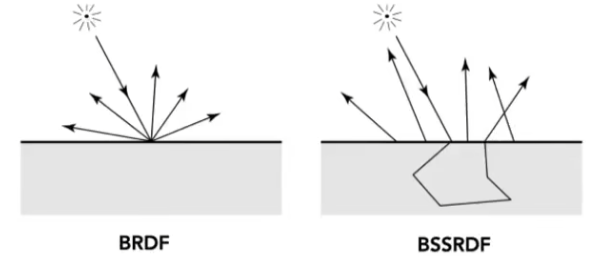
光从一点进入物体,在物体内部发生次表面散射(Subsurface Scattering)后离开物体;比如手指、玉石、胶体;
次表面散射可以认为是对 BRDF 的一种延伸,BSSRDF 除了接受入射方向和出射方向,也需要接受入射位置和出射位置;
对于 S ( x i , ω i , x o , ω o ) S(x_i,\omega_i,x_o,\omega_o) S ( x i , ω i , x o , ω o )
L o ( x o , ω o ) = ∫ A ∫ H 2 S ( x i , ω i , x o , ω o ) L i ( x i ω i ) cos θ i d ω i d A L_o(x_o,\omega_o)=\int_A\int_{H^2}S(x_i,\omega_i,x_o,\omega_o)L_i(x_i\omega_i)\cos\theta_i\mathrm{d}\omega_i\mathrm{d}A
L o ( x o , ω o ) = ∫ A ∫ H 2 S ( x i , ω i , x o , ω o ) L i ( x i ω i ) cos θ i d ω i d A
模型可以简化为在真实光源相对于着色点的对称点添加一个虚拟光源,被称为 Dipole Approximation,暂不赘述;
纤维(fibers)缠成股(ply),股缠绕成线(yarn),线织成布;
可以将织物视作空间中分布的体积,将其转化成对散射介质的渲染,这种方法速度较快;
也可以将纤维按毛发逻辑渲染,但是速度较慢;
对于三维物体内部纹理,如果直接存储会大量占用存储资源;我们选择对其进行程序化生成;通过一些 3D Noise 函数对于给定坐标返回纹理;
图形学主要有两种成像方式,即光栅化成像和光线追踪成像;现实成像是通过捕捉的方式进行的;
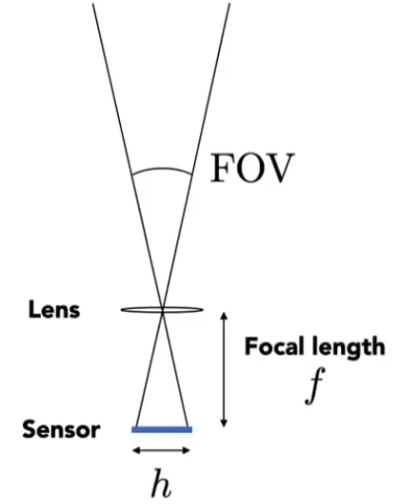
以垂直 FOV 为例
F O V = 2 arctan ( h 2 f ) FOV=2\arctan(\frac h{2f})
F O V = 2 arctan ( 2 f h )
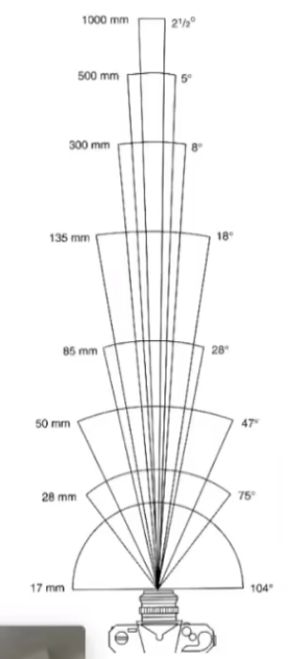
由于历史原因,以 36 × 24 mm 36\times24\text{mm} 3 6 × 2 4 mm
等效焦距的概念即为画幅下与标准画幅视场角相同的焦距;
Exposure = time × irradiance \text{Exposure}=\text{time}\times\text{irradiance} Exposure = time × irradiance
time 为曝光时间,由快门控制;irradiance 由透镜孔径和焦距控制;
快门、光圈、ISO略;
光圈 f 数定义为焦距与透光直径的比值;
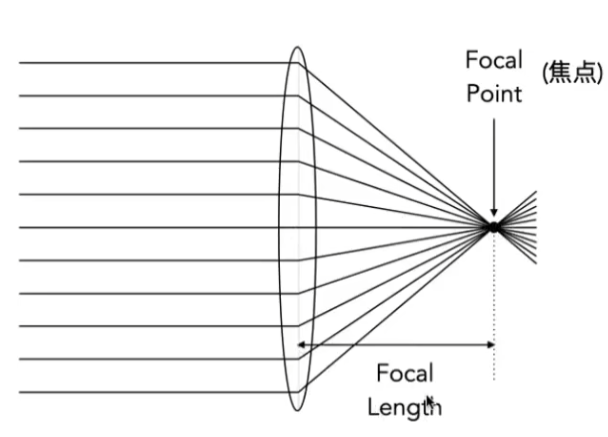
目前镜头都是由透镜组组成,课程内分析的是理想化的薄透镜,忽略其厚度;
特别地,假设薄透镜可以自由地改变焦距;
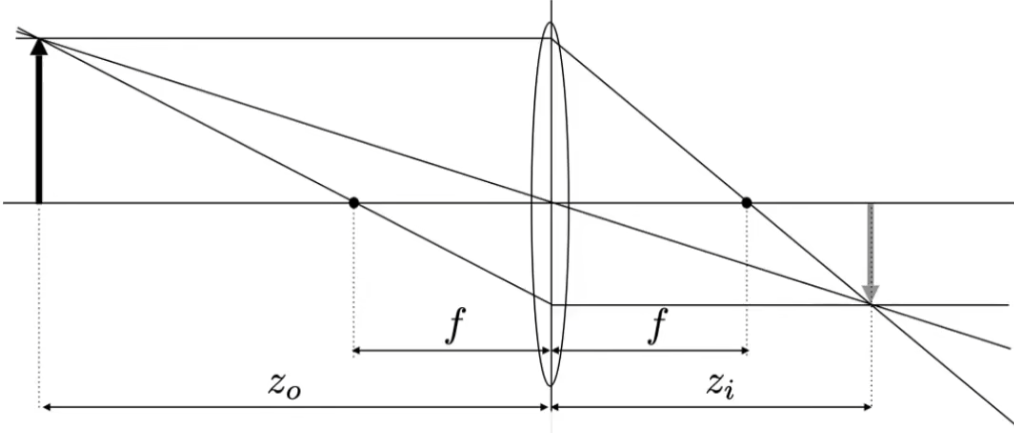
透镜的象距(z i z_i z i z o z_o z o
1 f = 1 z i + 1 z o \frac 1f=\frac1{z_i}+\frac 1{z_o}
f 1 = z i 1 + z o 1
可由相似三角形证明;
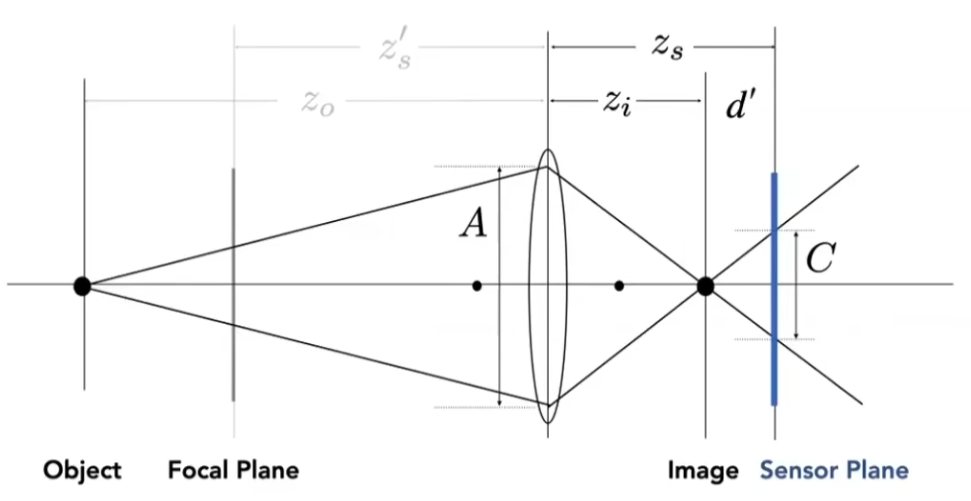
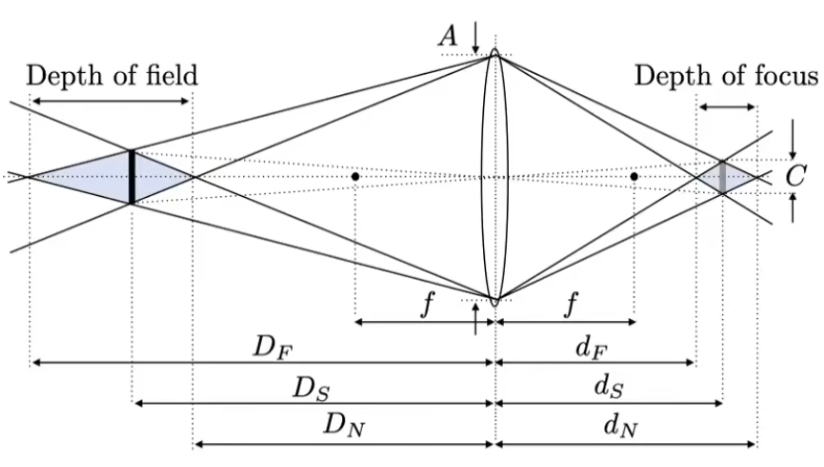
景深外物体的一点会在感光元件上形成弥散圆(光晕),假设光圈直径为 A ,f 数为 N ,有
C A = ∣ z s − z i ∣ z i C = f N ∣ z s − z i ∣ z i \frac CA=\frac{|z_s-z_i|}{z_i}\\
C=\frac fN\frac{|z_s-z_i|}{z_i}
A C = z i ∣ z s − z i ∣ C = N f z i ∣ z s − z i ∣
可以观察到,光圈直径越小(f数越大)弥散圆越小;
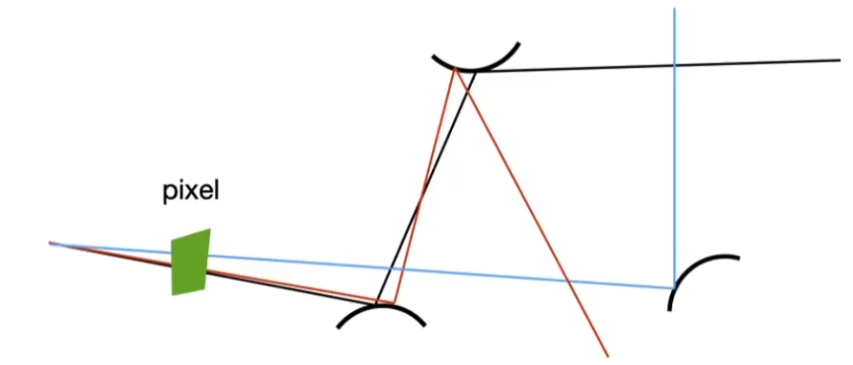
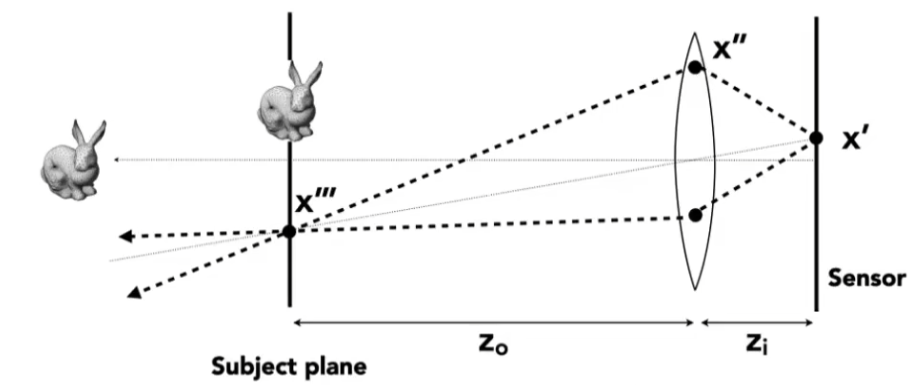
定义传感器尺寸、光圈大小、焦平面位置、透镜焦距(f f f z o z_o z o z i z_i z i
选择传感器的一个像素中心和透镜上的点进行连线,根据透镜公式,可以得出这束光离开棱镜时的方向和位置,按光线追踪进一步处理即可;
CoC 足够小(小于等于像素大小)时我们便认为该物体是清晰的,物体清晰成像的范围便是景深;
D O F = D F − D N D F = D s f 2 f 2 − N C ( D S − f ) D N = D s f 2 f 2 + N C ( D S − f ) DOF=D_F-D_N\\
D_F={D_sf^2\over f^2-NC(D_S-f)}\\
D_N={D_sf^2\over f^2+NC(D_S-f)}
D O F = D F − D N D F = f 2 − N C ( D S − f ) D s f 2 D N = f 2 + N C ( D S − f ) D s f 2
定义全光函数(The Plenoptic Function) P = ( θ , ϕ , λ , t , V X , V Y , V Z ) P=(\theta,\phi,\lambda,t,V_X,V_Y,V_Z) P = ( θ , ϕ , λ , t , V X , V Y , V Z ) V X , V Y , V Z V_X,V_Y,V_Z V X , V Y , V Z ( θ , ϕ ) (\theta,\phi) ( θ , ϕ ) λ \lambda λ
光场是对全光函数的一种简化:对于一个物体,在物体 / 包围盒表面上定义在任意位置向任意方向(外半球)的发光情况(4D);
光线除了点向定义,也可以由有序点对定义,所以光场也可以由两个平行的平面进行定义,光线便可以由两平面上的两点 ( u , v ) , ( s , t ) (u,v),(s,t) ( u , v ) , ( s , t )
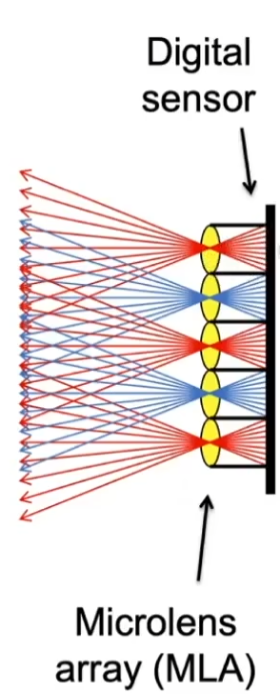
昆虫的复眼实际上进行的就是光场成像,将一个像素替换为一个透镜,使我们能够将打在这个像素上不同方向上的光记录在不同位置;
利用光场成像,我们可以在后期进行重新聚焦或移动相机的位置;
在每个透镜下存储的光线分别选择对应的光线即可进行重新成像;
光场相机存在分辨率不足、高成本等问题;
对于混合光,可以使用谱功率密度来描述不同波长光的分布;
SPD具有线性的性质,记光 A ,B 的谱功率密度分别为 SPDa ,SPDb ,将 A ,B 光混合得到的谱功率密度即为 SPDa + SPDb ;
颜色与 SPD 不完全相同,是人的感知;视网膜上主要有视锥细胞和视杆细胞两种感光细胞,其中视锥细胞主要感受光的颜色,视杆细胞主要感受光的强度;
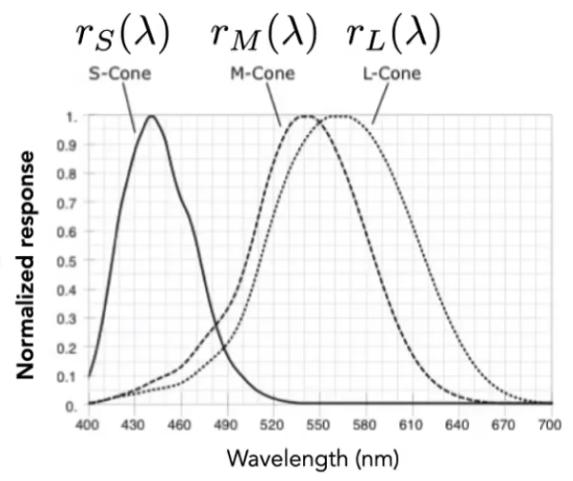
视锥细胞分为 S ,M ,L 三类,分别对三种波长的光响应最强;不同的人这三种视锥细胞的分布偏差很大;
对于给定 SPD 的色光 s ( λ ) s(\lambda) s ( λ )
S = ∫ r S ( λ ) s ( λ ) d λ M = ∫ r M ( λ ) s ( λ ) d λ L = ∫ r L ( λ ) s ( λ ) d λ S=\int r_S(\lambda)s(\lambda)\mathrm{d}\lambda\\
M=\int r_M(\lambda)s(\lambda)\mathrm{d}\lambda\\
L=\int r_L(\lambda)s(\lambda)\mathrm{d}\lambda
S = ∫ r S ( λ ) s ( λ ) d λ M = ∫ r M ( λ ) s ( λ ) d λ L = ∫ r L ( λ ) s ( λ ) d λ
对于两个不同 SPD 的色光,在我们的感知下可能相同;
颜色匹配过程正是利用率同色异谱现象;
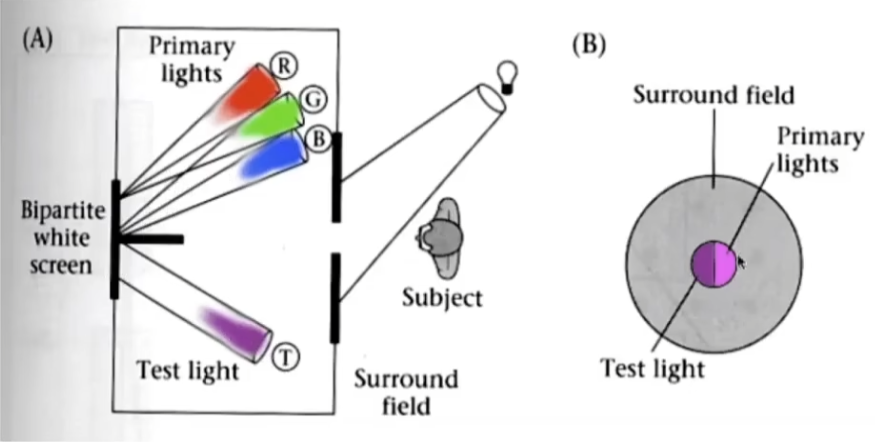
加色系统是给定一组有自己频谱分布的主光(如 s R ( λ ) , s G ( λ ) , s B ( λ ) s_R(\lambda),s_G(\lambda),s_B(\lambda) s R ( λ ) , s G ( λ ) , s B ( λ ) R s R ( λ ) + G s G ( λ ) + B s B ( λ ) Rs_R(\lambda)+Gs_G(\lambda)+Bs_B(\lambda) R s R ( λ ) + G s G ( λ ) + B s B ( λ )
认为左右颜色相同时即完成了颜色匹配;
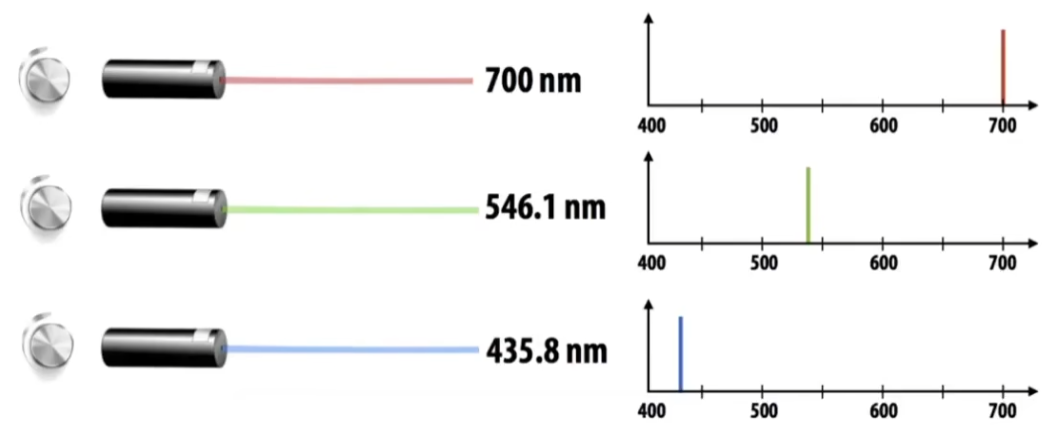
CIE规定了三种波长作为 CIE RGB 的主光
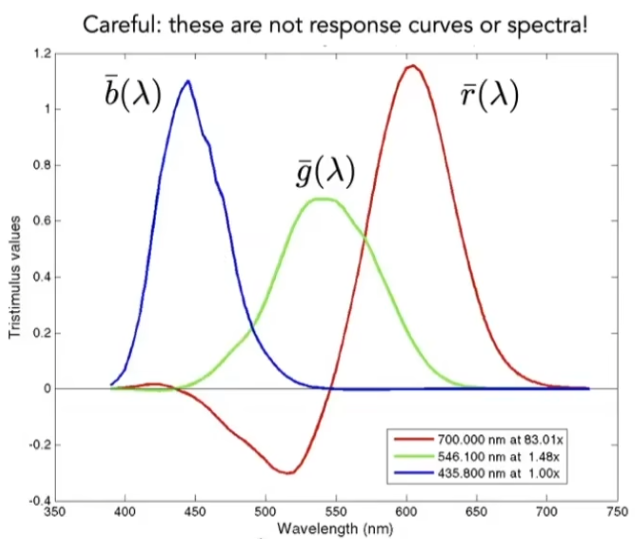
对于任意波长的单色光,有匹配函数
对于给定 SPD 的色光 s ( λ ) s(\lambda) s ( λ )
R CIE RGB = ∫ λ s ( λ ) r ‾ ( λ ) d λ G CIE RGB = ∫ λ s ( λ ) g ‾ ( λ ) d λ B CIE RGB = ∫ λ s ( λ ) b ‾ ( λ ) d λ R_{\text{CIE RGB}} = \int_\lambda s(\lambda)\overline r(\lambda)\mathrm d\lambda\\
G_{\text{CIE RGB}} = \int_\lambda s(\lambda)\overline g(\lambda)\mathrm d\lambda\\
B_{\text{CIE RGB}} = \int_\lambda s(\lambda)\overline b(\lambda)\mathrm d\lambda\\
R CIE RGB = ∫ λ s ( λ ) r ( λ ) d λ G CIE RGB = ∫ λ s ( λ ) g ( λ ) d λ B CIE RGB = ∫ λ s ( λ ) b ( λ ) d λ
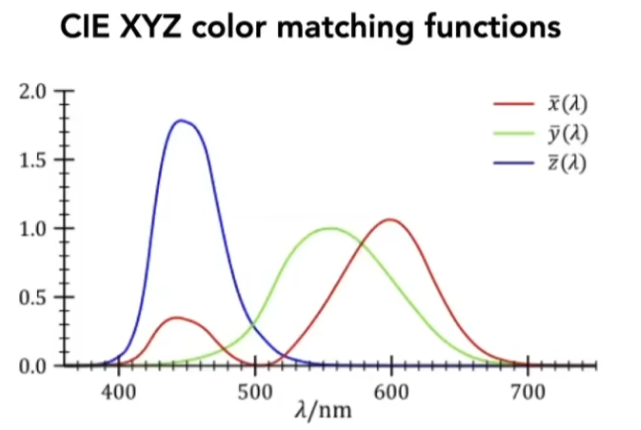
此外,还有 CIE XYZ 颜色匹配系统,首先定义色彩匹配函数
我们观察到其中 y 在不同波长均有分布且对称,在一定程度上可以代表颜色的 luminance ;
我们将 XYZ 归一化,有
x = X X + Y + Z y = Y X + Y + Z z = Z X + Y + Z x=\frac X{X+Y+Z}\\
y=\frac Y{X+Y+Z}\\
z=\frac Z{X+Y+Z}
x = X + Y + Z X y = X + Y + Z Y z = X + Y + Z Z
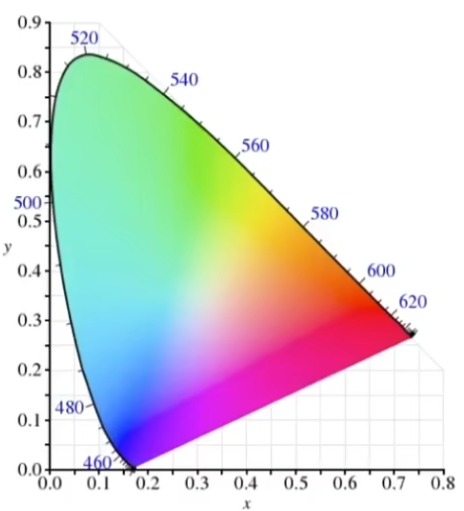
我们选择 x ,y ,对应位置显示特定的 Y 值下的颜色,便形成了颜色玛蹄图
在 ( 1 3 , 1 3 ) (\frac 13,\frac 13) ( 3 1 , 3 1 )
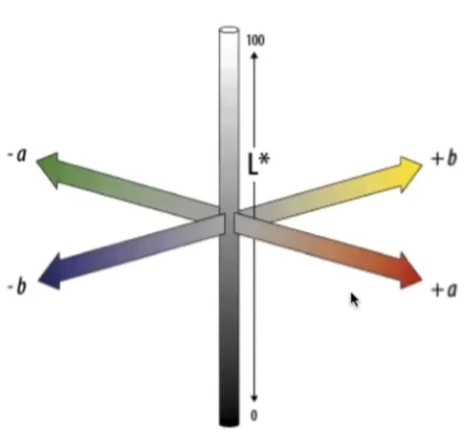
L 轴为亮度轴,a 轴为红轴, b轴为黄轴;
其中红轴上的红绿两端互为互补色,黄蓝两端互为互补色;
印刷中常用的一种颜色空间,引入黑色是为了控制印刷成本;
最基础的单元即是由弹簧(劲度系数 k s k_s k s
f a → b = k s b − a ∣ ∣ b − a ∣ ∣ ( ∣ ∣ b − a ∣ ∣ − l ) f b → a = − f a → b f_{a\to b}=k_s\frac{b-a}{||b-a||}(||b-a||-l)\\
f_{b\to a} = -f_{a\to b}
f a → b = k s ∣ ∣ b − a ∣ ∣ b − a ( ∣ ∣ b − a ∣ ∣ − l ) f b → a = − f a → b
上述模型会出现无限振动的问题,动能和势能永远相互转化,需要添加摩擦力;
记 x ˙ \dot x x ˙ x ¨ \ddot x x ¨
f = − k d b − a ∣ ∣ b − a ∣ ∣ ( b ˙ − a ˙ ) b − a ∣ ∣ b − a ∣ ∣ f=-k_d\frac{b-a}{||b-a||}(\dot b-\dot a)\frac{b-a}{||b-a||}
f = − k d ∣ ∣ b − a ∣ ∣ b − a ( b ˙ − a ˙ ) ∣ ∣ b − a ∣ ∣ b − a
其中 b − a ∣ ∣ b − a ∣ ∣ ( b ˙ − a ˙ ) \frac{b-a}{||b-a||}(\dot b-\dot a) ∣ ∣ b − a ∣ ∣ b − a ( b ˙ − a ˙ ) a b ‾ \overline{ab} a b b − a ∣ ∣ b − a ∣ ∣ \frac{b-a}{||b-a||} ∣ ∣ b − a ∣ ∣ b − a a b → \overrightarrow{ab} a b
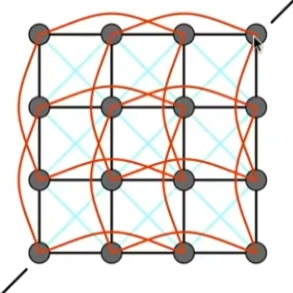
通过此种形式的模型即可对布料进行一定程度的仿真
其中蓝线比黑线更强,用于抵消斜向形变,红线比黑线更弱,用于抵消弯折形变;
除了质点弹簧系统,也可以使用有限元方法(Finite Element Method ,FEM)进行模拟;
粒子系统被用于模拟灰尘、雾、流体、鸟群等;
粒子受力比较复杂,可能会受到引力、电磁力、虚拟弹簧弹力、推进力、粒子间摩擦力。粒子间粘滞力、粒子间碰撞、空气阻力、与容器或固定物的碰撞、与动态物体的碰撞等等;
通过定义不同的关节来模拟人体的结构;
有三种不同的关节:销(Pin)(一自由度旋转)、球(Ball)(二自由度旋转)、移动关节(Prismatic joint)(平移);
对于给定关节组的参数(类型、长度、旋转角度等),可以很轻松地算出关节末端的位置;
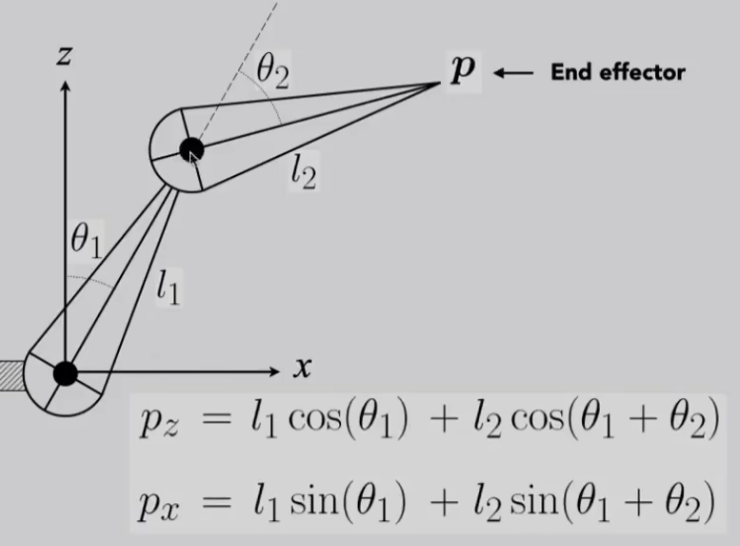
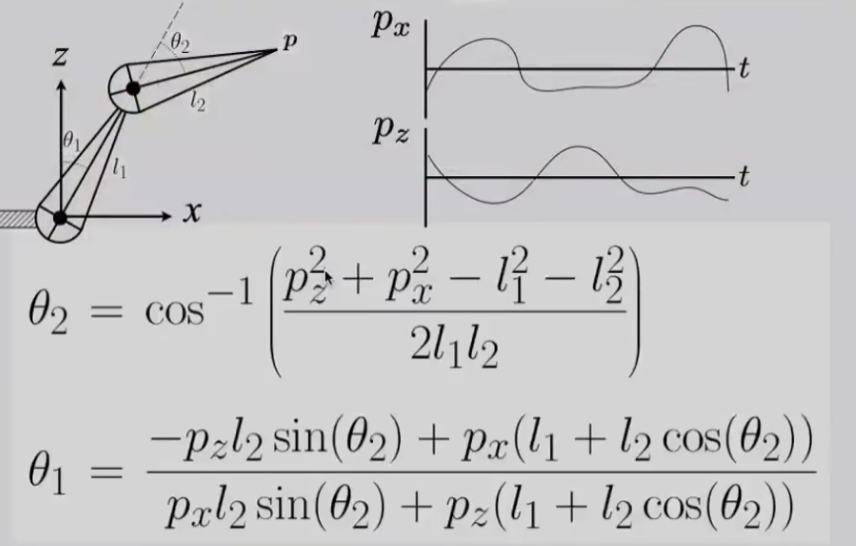
对于两个销关节,有参数 l 1 , θ 1 , l 2 , θ 2 l_1,\theta_1,l_2,\theta_2 l 1 , θ 1 , l 2 , θ 2
通过定义关节组末端的位置和关节组的类型、长度等参数,反向确定关节组的旋转角度等其他自由度;
对于长度为 l 1 , l 2 l_1,l_2 l 1 , l 2 ( p x , p z ) (p_x,p_z) ( p x , p z )
会涉及到多解和无解的问题;
Rigging 是逆运动学的一个应用,类似操控布偶一样控制关节;对人物模型添加若干控制点,通过对控制点的控制来控制人物模型;
通过在真人身上定义并捕捉控制点,将真人的动作映射到虚拟人物上;
真实感强、获取快速;但昂贵且设备复杂,真人演员可能无法满足动画需要;
其中光学动补应用较为广泛;
假设物体的运动由速度场决定,速度场可以定义为关于位置和时间的函数 v ( x , t ) v(x,t) v ( x , t )
对于物体有
d x t = x ˙ = v ( x , t ) {\mathrm dx\over\mathrm t}=\dot x=v(x,t)
t d x = x ˙ = v ( x , t )
这种写法被称为一阶常微分方程;
Δ t \Delta t Δ t
x t + Δ t = x t + Δ t x ˙ t x ˙ t + Δ t = x ˙ t + Δ t x ¨ t x^{t+\Delta t}=x^t+\Delta t\dot x^t\\
\dot x^{t+\Delta t}=\dot x^t+\Delta t\ddot x^t
x t + Δ t = x t + Δ t x ˙ t x ˙ t + Δ t = x ˙ t + Δ t x ¨ t
这种方法并不准确,不准确程度会随着 Δ t \Delta t Δ t
解决不稳定性的问题可以通过以下方法;
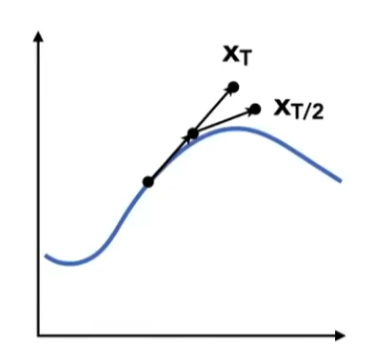
用某个 Δ t \Delta t Δ t
x m i d = x ( t ) + Δ t / 2 ⋅ v ( x ( t ) , t ) x ( t + Δ t ) = x ( t ) + Δ t ⋅ v ( x m i d , t ) x_{mid} = x(t)+\Delta t/2\cdot v(x(t),t)\\
x(t+\Delta t) = x(t)+\Delta t\cdot v(x_{mid},t)
x m i d = x ( t ) + Δ t / 2 ⋅ v ( x ( t ) , t ) x ( t + Δ t ) = x ( t ) + Δ t ⋅ v ( x m i d , t )
比较显示欧拉方法计算出的 x ( t + Δ t ) x(t+\Delta t) x ( t + Δ t ) x ( t + Δ t / 2 ) ( t + Δ t / 2 + Δ t / 2 ) x(t+\Delta t/2)(t+\Delta t/2+\Delta t/2) x ( t + Δ t / 2 ) ( t + Δ t / 2 + Δ t / 2 ) Δ t = Δ t / 2 \Delta t=\Delta t/2 Δ t = Δ t / 2
不同于显式欧拉方法,隐式欧拉方法使用下个时刻的参数进行模拟;
x t + Δ t = x t + Δ t x ˙ t + Δ t x ˙ t + Δ t = x ˙ t + Δ t x ¨ t + Δ t x^{t+\Delta t}=x^t+\Delta t\dot x^{t+\Delta t}\\
\dot x^{t+\Delta t}=\dot x^t+\Delta t\ddot x^{t+\Delta t}
x t + Δ t = x t + Δ t x ˙ t + Δ t x ˙ t + Δ t = x ˙ t + Δ t x ¨ t + Δ t
实际上需要解出下一个时刻的参数;
Runge-Kutta 方法中有一个四阶稳定性的算法名为 RK4 ;
d y d t = f ( t , y ) y n + 1 = y n + 1 6 + Δ t ( k 1 + 2 k 2 + 2 k + 3 + k 4 ) t n + 1 = t n + Δ t k 1 = f ( t n , y n ) k 2 = f ( t n + Δ t 2 , y n + Δ t k 1 2 ) k 3 = f ( t n + Δ t 2 , y n + Δ t k 2 2 ) k 4 = f ( t n + Δ t , y n + Δ t k 3 ) {\mathrm dy\over\mathrm dt}=f(t,y)\\
y_{n+1}=y_n+\frac 16 + \Delta t(k_1+2k_2+2k+3+k_4)\\
t_{n+1}=t_n+\Delta t\\
k_1=f(t_n,y_n)\\
k_2=f(t_n+\frac {\Delta t}2,y_n+\Delta t\frac {k_1}2)\\
k_3=f(t_n+\frac {\Delta t}2,y_n+\Delta t\frac {k_2}2)\\
k_4=f(t_n+\Delta t,y_n+\Delta tk_3)
d t d y = f ( t , y ) y n + 1 = y n + 6 1 + Δ t ( k 1 + 2 k 2 + 2 k + 3 + k 4 ) t n + 1 = t n + Δ t k 1 = f ( t n , y n ) k 2 = f ( t n + 2 Δ t , y n + Δ t 2 k 1 ) k 3 = f ( t n + 2 Δ t , y n + Δ t 2 k 2 ) k 4 = f ( t n + Δ t , y n + Δ t k 3 )
此类方法并不是基于物理的,速度更快,不保证能量守恒;
对误差可以定义为每步的截断误差(local truncation error)和累积误差(total accumulated error);
通过描述误差与 Δ t \Delta t Δ t
其中隐式欧拉方法是一阶的,记 Δ t = h \Delta t=h Δ t = h O ( h 2 ) O(h^2) O ( h 2 ) O ( h ) O(h) O ( h )
刚体不会发生形变;
刚体模拟在质点模拟的基础上,增加了角速度和角加速度
d d t ( X θ X ˙ ω ) = ( X ˙ ω F / M Γ / I ) {\mathrm d\over\mathrm dt}
\begin{pmatrix}
X\\
\theta\\
\dot X\\
\omega
\end{pmatrix}
=
\begin{pmatrix}
\dot X\\
\omega\\
F/M\\
\Gamma/I
\end{pmatrix}
d t d ⎝ ⎜ ⎜ ⎛ X θ X ˙ ω ⎠ ⎟ ⎟ ⎞ = ⎝ ⎜ ⎜ ⎛ X ˙ ω F / M Γ / I ⎠ ⎟ ⎟ ⎞
即位置、角度、速度、角速度对时间的导数分别为速度、角速度、加速度、角加速度(力矩/转动惯量);
认为水体是由不可压缩的刚体小球组成的;对于密度不正确的区域,通过移动小球来修正;为了计算密度,需要得知某点的密度关于所有粒子位置变化的导数;通过梯度下降来修正密度;
此处欧拉方法与前述解拉格朗日方程的欧拉方法不同;
拉格朗日方法是“质点法”,通过对所有质点的正确模拟来达到对全局的模拟;
欧拉方法是“网格法”,针对于模拟空间网格本身的属性随时间变化的结果;
物质点方法(Material Point Method ,MPM)结合了这两种方法;