2022牛客暑期多校训练营9（ABEG）

题集链接；

A Car Show

题意

给定长度为n，由数字1~m组成的数列，问包含全部m个数字的子串个数；

思路

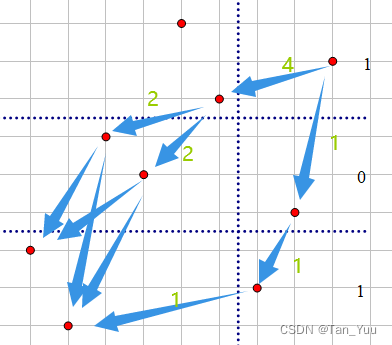
定位每一个左端点，向右寻找最近的符合要求的右界，得到最小子串，右界从此处开始直至序列末尾均合法，依此更新答案；

更新答案后左界左移，再次执行以上过程；

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
int a[100005];
int main()
{
    int n, m;
    cin >> n >> m;
    ll ans = 0;
    for (int i = 1; i <= n; i++)
    {
        scanf("%d", &a[i]);
    }
    int l = 1, r = 1, ct = 0;
    unordered_map<int, int> mp;
    for (; r <= n; r++)
    {
        mp[a[r]]++;
        if (mp[a[r]] == 1)
        {
            ct++;
        }
        while (ct == m && l <= r)
        {
            ans += n - r + 1;
            mp[a[l]]--;
            if (!mp[a[l]])
                ct--;
            l++;
        }
    }
    cout << ans;
    return 0;
}

B Two Frogs

概率期望

题意

有n个荷叶排成一列，每个荷叶有属性值 aia_i ，当青蛙在i号荷叶上时，下一步可以跳到 [i+1,i+ai][i+1,i+a_i] 号荷叶上，求两只青蛙从1号荷叶起经过相同次数的跳动，同时到达n号荷叶的概率；

思路

考虑 q[m][x]q[m][x] 为跳m次到达x号的概率，则有 q[m][x]=∑i+1⩽x⩽i+a[i]q[m−1][i]a[i]q[m][x]=\sum_{i+1\leqslant x\leqslant i+a[i]}\frac {q[m-1][i]}{a[i]} ；
答案即为 ∑i=1n−1q[i][n]2\sum_{i=1}^{n-1}q[i][n]^2；

考虑计算过程，由于对于每一个 q[m][x]q[m][x] ，更新的是 q[m][x+i],i∈[1,a[x]]q[m][x+i],i\in[1,a[x]] 连续区间的值，我们可以用差分优化这个操作；

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll M = 998244353;
ll q[8003][8003];
int exs[8003];
ll inv[8003];
int a[8003];

long long Q_power(long long a, long long b = M - 2)
{
    long long res = 1;
    while (b)
    {
        if (b & 1)
            res = res * a % M;
        b >>= 1;
        a = a * a % M;
    }
    return res;
}

int main()
{
    int n;
    cin >> n;
    for (int j = 1; j <= n; j++)
    {
        inv[j] = Q_power(j);
    }
    for (int i = 1; i <= n; i++)
        exs[i] = 10000;
    exs[1] = 0;
    for (int i = 1; i < n; i++)
    {
        scanf("%d", &a[i]);
        for (int j = 1; j <= a[i]; j++)
        {
            exs[i + j] = min(exs[i + j], exs[i] + 1);
        }
    }
    q[1][0]=1;
    for (int i = 1; i <= n; i++)
    {
        for (int j = exs[i]; j <= i - 1; j++)
        {
            q[i][j] = q[i - 1][j] + q[i][j];
            q[i][j] %= M;
            ll p = q[i][j] * inv[a[i]];
            q[i + 1][j + 1] = (q[i + 1][j + 1] + p) % M;
            q[i + a[i] + 1][j + 1] = (q[i + a[i] + 1][j + 1] - p) % M;
        }
    }
    ll ans = 0;
    for (int i = exs[n]; i < n; i++)
        ans += q[n][i] * q[n][i], ans %= M;
    printf("%lld", ans);
    return 0;
}

E Longest Increasing Subsequence

构造

题意

构造长度为 n⩽100n\leqslant100 的排序，使得最长上升子序列恰好为m个；

思路

将m进行二进制拆分，考虑以下构造方法：

image.png

image.png

image.png

对于每层最右侧的点，其向下的支是累计下层计数，向左的支是累计本层计数；

依照此策略，可以在 3log⁡(n)3\log(n) 的长度内构造完成；

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
#include <bits/stdc++.h>
using namespace std;
int main()
{
    int n, t;
    cin >> t;
    while (t--)
    {
        int ct = 1;
        vector<int> r(90);
        cin >> n;
        for (int i = 0; i < 30; i++)
        {
            if ((n >> i) & 1)
            {
                r[2 * i + 1] = ct++;
                r[60 + i] = ct++;
                r[2 * i] = ct++;
            }
            else
            {
                r[60 + i] = ct++;
                r[2 * i + 1] = ct++;
                r[2 * i] = ct++;
            }
        }
        printf("90\n");
        for(int i=0;i<90;i++)
        {
            printf("%d%c",r[i]," \n"[i == 89]);
        }
    }
}

G Magic Spells

manacher，二分

题意

给定k个字符串，找出在每个串都出现的回文串数量；

思路

首先考虑马拉车算法，找出所有字符串进行统计，使用map将字符串从哈希值映射到最近出现时间（1~k）；

果不其然地T了，接下来考虑优化：

首先进行剪枝，在固定圆心从大到小遍历半径的过程中，如果发现某串最近出现时间已经是当前，那么该圆心下半径更小的串就不用考虑了；

依然T，继续优化：

考虑二分，对于固定圆心从大到小遍历半径的过程中，存在分界半径i，半径小于i时最近出现时间均是上串，大于i时最近出现时间均早于上串，以此二分快速确定有效半径；

单哈希可以过；

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
#include <bits/stdc++.h>

using namespace std;
typedef long long ll;
const int maxn = 3e5 + 5;
char s[maxn * 2];
string str;
int d[maxn * 2], len;
void getstr() {
   str.clear();
   int k = 0;
   str += '{';
   k++;
   for (int i = 0; i < len; i++) {
      str += '}';
      str += s[i];
      k += 2;
   }
   str += '}';
   k++;
   len = k;
}
int manacher() {
   int mx = 0, id;
   int maxx = 0;
   for (int i = 0; i < len; i++) {
      if (i < mx)
         d[i] = min(mx - i + 1, d[2 * id - i]);
      else
         d[i] = 1;
      while (i + d[i] <= str.size() && i - d[i] >= 0 &&
             str[i + d[i]] == str[i - d[i]])
         d[i]++;
      if (d[i] + i - 1 > mx) {
         mx = d[i] + i - 1;
         id = i;
         maxx = max(maxx, d[i]);
      }
   }
   return (maxx - 1);
}

const long long MAGIC = 1e12 + 39;
long long hsh[maxn * 2];
void init() {
   hsh[0] = 1;
   for (int i = 1; i != maxn * 2; i++) {
      hsh[i] = hsh[i - 1] * 1013ll % MAGIC;
   }
}

long long str_hsh[maxn * 2];
void _hsh() {
   str_hsh[0] = str[0] - '_';
   for (int i = 1; i != str.length(); i++) {
      str_hsh[i] = (str_hsh[i - 1] * 1013ll + str[i] - '_') % MAGIC;
   }
}

long long get_hash(int l, int r) {
   if (l == 0) return str_hsh[r];
   auto fna = str_hsh[r] -
              __int128_t(1) * str_hsh[l - 1] * hsh[r - l + 1] % MAGIC;
   if (fna < 0) fna += MAGIC;
   return fna % MAGIC;
}

long long _len_hash(long long raw, int len) {
   return raw * (long long)3e5 + len;
}

int main() {
   int k;
   long long ans = 0;
   cin >> k;
   init();
   unordered_map<ll, int> mp;
   for (int kki = 0; kki < k; kki++) {
      cin >> s;
      len = strlen(s);
      getstr();
      _hsh();
      manacher();
      for (int i = 0; i < len; i++) {
         // printf("%c%d",str[i],d[i]);
         for (int j = d[i]; j >= 1; j--) {
            auto hsh = get_hash(i, i + j - 1);

            if (mp[hsh] == kki + 1)
               break;
            else if (mp[hsh] != kki) {
               int l = 1, r = j;

               int res = 0;
               while (l <= r) {
                  j = (l + r) / 2;
                  hsh = get_hash(i, i + j - 1);
                  if (mp[hsh] < kki) {
                     res = j;
                     r = j - 1;
                  } else {
                     l = j + 1;
                  }
               }
               j = res;
               // cerr << "IN binary " << j << '\n';
            } else if (mp[hsh] == kki) {
               mp[hsh] = kki + 1;
               if (mp[hsh] == k &&
                   !(str[i + j - 1] == '}' || str[i + j - 1] == '{'))
                  ans++;
               // break;
            }

            // cerr << str.substr(i, j) << " " << hsh << " " <<
            // mp[hsh]
            //      << endl;

            // printf("*%lld %d\n", mp[hsh],kki);
         }
      }
   }
   printf("%lld\n", ans);
   return 0;
}
算法竞赛 > 比赛与题集
2022牛客暑期多校训练营9（ABEG）
https://tanyuu.github.io/2022.07-12/2022牛客暑期多校训练营9（ABEG）/
作者
F Juny
发布于
2022年8月16日
许可协议