2022牛客暑期多校训练营1（ACDGIJ）

题集链接；

文字题解、视频题解；

A Villages: Landlines

区间和并

思路

一维线上有若干个建筑物，每个建筑物有自己的覆盖范围，问所有建筑物间空白区域长度（题目描述有些复杂了）；

每个建筑物对应了一段区间，求出合并后区间间的长度即可；

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
pair<ll, ll> ps[200005];
int main()
{
    int n;
    ll p, q;
    cin >> n;
    for (int i = 1; i <= n; i++)
    {
        scanf("%lld%lld", &p, &q);
        ps[i].first = p - q, ps[i].second = p + q;
    }
    sort(ps + 1, ps + n + 1);
    ll l, r, ans = 0;
    l = ps[1].first, r = ps[1].second;
    for (int i = 2; i <= n; i++)
    {
        if (ps[i].first <= r)
            r = max(ps[i].second, r);
        else
        {
            ans += ps[i].first - r;
            l = ps[i].first, r = ps[i].second;
        }
    }
    cout << ans;
    return 0;
}

C Grab the Seat!

计算几何（？）

思路

文字描述比较繁琐~
以样例2的第一次变化为例：
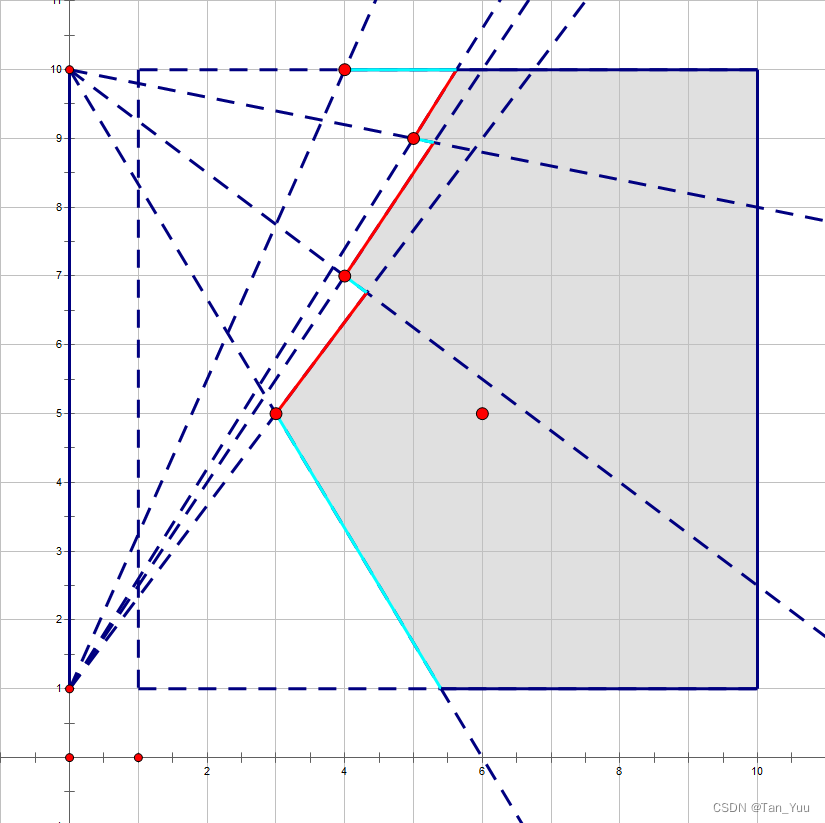
image.png

我们可以观察到，灰色区域的所有点（含边界）都不是好点，而影响灰色边界范围的，仅是每一行最靠前的一个有人位；

我们将灰色区域的“可变边界”（由有人位贡献的边界）划分成红色和青色两部分，然后可以通过从下至上和从上至下两次遍历维护每行的好点数；

对于每次遍历，我们只需要记录已遍历部分中斜率最大/最小的边界线，由其与此行的交点坐标限定此行的好点数。在维护边界线时，注意边界情况（斜率为0）；

两次遍历后，累加每行的好点数即可得到答案，每次查询的时间复杂度为O(n)O(n)；

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef long double ld;
const ll M = 1e9 + 7;
const double eps = 1e-6;
pair<int, int> p[200005];
set<int> lne[200005];
ll bar[200005];
ll cnt(int n, int m)
{
    int mnl = n + 1, mxl = 0;
    for (int i = 1; i <= m; i++)
    {
        bar[i] = n;
        if (!lne[i].empty())
            mnl = min(mnl, i), mxl = max(mxl, i);
    }
    pair<double, double> now = {1, 0};
    for (int i = 1; i <= m; i++)
    {
        if (!lne[i].empty())
        {
            pair<double, double> tmp = {(double)*lne[i].begin(), (double)i};
            if ((tmp.second - 1) / tmp.first > (now.second - 1) / now.first)
                now = tmp;
        }
        ll lim = n;
        if (fabs(now.second) > eps) //边界点有效
        {
            if (fabs(now.second - 1) > eps) //边界点不临边
                lim = (i - 1.0) * now.first / (now.second - 1) - eps;
            else if (i == 1) //边界点临边且该行为边
            {
                lim = now.first - 1 + eps;
            }
            bar[i] = min(bar[i], lim);
        }
        // printf("\\%d\n", bar[i]);
    }
    now = {1, m + 1};
    for (int i = m; i >= 1; i--)
    {
        if (!lne[i].empty())
        {
            pair<double, double> tmp = {(double)*lne[i].begin(), (double)i};
            if ((tmp.second - m) / tmp.first < (now.second - m) / now.first)
                now = tmp;
        }
        ll lim = n;
        if (fabs(now.second - m - 1) > eps) //边界点有效
        {
            if (fabs(now.second - m) > eps) //边界点不临边
                lim = (i - m) * now.first / (now.second - m) - eps;
            else if (i == m) //边界点临边且该行为边
            {
                lim = now.first - 1 + eps;
            }
            bar[i] = min(bar[i], lim);
        }
    }
    ll ans = 0;
    for (int i = 1; i <= m; i++)
    {
        // printf("*%d\n", bar[i]);
        ans += bar[i];
    }
    return ans;
}
int main()
{
    int n, m, k, q;
    cin >> n >> m >> k >> q;
    for (int i = 1; i <= k; i++)
    {
        scanf("%d%d", &p[i].first, &p[i].second);
    }
    for (int i = 1; i <= k; i++)
    {
        lne[p[i].second].insert(p[i].first);
    }
    while (q--)
    {
        pair<int, int> tmp;
        int cg;
        scanf("%d%d%d", &cg, &tmp.first, &tmp.second);
        lne[p[cg].second].erase(p[cg].first);
        p[cg] = tmp;
        lne[tmp.second].insert(tmp.first);
        printf("%lld\n", cnt(n, m));
    }
    return 0;
}

D Mocha and Railgun

计算几何

思路

有一个以原点为圆心，半径给定的圆，圆内给定一个点Q和长度d，以Q为中点，2d为长度在圆内构造线段（数据保证线段一定不会出圆），问能够投影在线段某一侧（无所谓）的圆周最大长度；

不难想象（没有进行证明），在线段方向为径向时，题求长度最长；

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef long double ld;
const ld eps = 1e-12;
const ld PI = acos(-1.0);
int sign(ld x)
{
    if (fabs(x) < eps)
        return 0;
    if (x > 0)
        return 1;
    else
        return -1;
}
int main()
{
    int t;
    cin >> t;
    while (t--)
    {
        ld r, x, y, d, dis1, dis2;
        scanf("%Lf%Lf%Lf%Lf", &r, &x, &y, &d);
        double disq = sqrt(x * x + y * y);
        dis1 = disq - d;
        dis2 = disq + d;
        ld ac1, ac2;
        ac1 = acos(dis1 / r);
        ac2 = acos(dis2 / r);
        printf("%.12Lf\n", (ac1 - ac2) * r);
    }
    return 0;
}

G Lexicographical Maximum

贪心

思路

给定一个数字，求小于等于它的数字中，字典序最大的数字；

贪心策略：如果该数满足除最后一位外都为9，则输出该数。否则输出相比此数少一位的9；

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
#include <bits/stdc++.h>
using namespace std;

int main()
{
    string s;
    cin >> s;
    bool f = true;
    for (int i = 0; i != s.length() - 1; i++)
    {
        if (s[i] != '9')
        {
            f = false;
            break;
        }
    }
    if (f)
        cout << s << '\n';
    else
        for (int i = 0; i != s.length() - 1; i++)
        {
            cout << 9;
        }
    return 0;
}

I Chiitoitsu

概率期望

思路

一副牌有34种牌，每种四张，在排队中给出13张初始手牌，保证初始手牌中相同的牌不超过两张；

每轮做如下操作：

  1. 在牌堆中随机抽出一张牌，加入手牌；
  2. 如果手牌中满足有不同种类的7对相同牌（11，33，22，77，99……）则结束游戏；
  3. 否则弃掉一张牌，保持13张手牌；

给出初始手牌，问最优（最快结束）策略下结束游戏的轮数期望；

对于给定两个参数：牌堆剩余牌数l & 待配对牌数n，对于所有l,n相同的情况，此时到游戏结束的轮数期望也相同；

我们定义给定l,n的轮数期望为 f(l,n)f(l,n) ，则有递归式：

f(l,n)=1+{3nlf(l−1,n−2)if n>10else+{l−3nlf(l−1,n)if l>3n0elsef(l,n)=1+\begin{cases} \frac{3n}{l}f(l-1,n-2)&\text{if }n>1\\ 0&\text{else} \end{cases}+ \begin{cases} \frac{l-3n}{l}f(l-1,n)&\text{if }l>3n\\ 0&\text{else} \end{cases}

直观来说，前面的cases描述的是抽到待配对牌中的一张，后面的cases描述的是没有抽到；

记忆化存储 f(l,n)f(l,n) 的值即可；

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef long double ld;
const ll M = 1e9 + 7;
ll qm(ll a, ll b = M - 2)
{
    ll ans = 1;
    for (; b; b >>= 1)
    {
        if (b & 1)
            ans = ans * a % M;
        a = a * a % M;
    }
    return ans;
}
ll tab[150][14];
ll f(ll lft, ll ndd)
{
    if (tab[lft][ndd])
        return tab[lft][ndd];
    ll ans = 1;
    if (ndd > 1)
        ans += 3 * ndd * qm(lft) % M * f(lft - 1, ndd - 2) % M;
    if (lft > 3 * ndd)
        ans += (lft - 3*ndd) * qm(lft) % M * f(lft - 1, ndd) % M;
    ans %= M;
    return tab[lft][ndd] = ans;
}
int main()
{
    int t,tt=1;
    cin >> t;
    while (t--)
    {
        string g;
        int cnt = 0;
        map<string, int> mp;
        cin >> g;
        for (int i = 0; g[i]; i += 2)
        {
            mp[g.substr(i, 2)]++;
            if (mp[g.substr(i, 2)] == 2)
                cnt++;
        }
        printf("Case #%d: %lld\n", tt++, f(123, 13 - 2 * cnt));
    }
    return 0;
}

J Serval and Essay

拓扑排序 并查集

思路

给出一个无重边自环的有向图，选定某一点作为起点，以拓扑排序的逻辑进行扩展，求出扩展后点数最大值；

拓扑排序优化失败，之后并查集暴力过；

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef long double ld;
const ll M = 1e9 + 7;
const double eps = 1e-6;

vector<int> rod[200005];
int cnt[200005];//cnt实际无意义
pair<int, int> bel[200005];
int ord[200005];
inline int read()
{
    int v = 0, c = 1;
    char ch = getchar();
    while (!isdigit(ch))
    {
        if (ch == '-')
            c = -1;
        ch = getchar();
    }
    while (isdigit(ch))
    {
        v = v * 10 + ch - 48;
        ch = getchar();
    }
    return v * c;
}
int find(int x)
{
    if (bel[x].first == x)
        return x;
    else
        return bel[x].first = find(bel[x].first);
}
bool check(int x)
{
    if (find(x) != x || rod[x].empty()) //如果该点不独立或这个点没有父节点
        return false;
    int now = find(rod[x][0]);
    for (auto v : rod[x]) //判断是否所有父节点都在一个集合里
    {
        if (now != find(v))
            return false;
    }
    if (now == x) //判断父节点是否与自己在一个集合
        return false;
    return true;
}
int main()
{
    int t, n, k, q, tt = 1;
    cin >> t;
    while (t--)
    {
        scanf("%d", &n);
        for (int i = 1; i <= n; i++)
            rod[i].clear(), bel[i] = {i, 1};
        for (int i = 1; i <= n; i++)
        {
            // scanf("%d", &cnt[i]);
            cnt[i] = read();
            for (int j = 1; j <= cnt[i]; j++)
            {
                q = read();
                rod[i].push_back(q);
            }
        }
        for (int i = 1; i <= n; i++)
        {
            ord[i] = i;
        }
        // random_shuffle(ord + 1, ord + n + 1);随机化后会超时
        int ans = 1;
        while (1)
        {
            // printf("*");
            int flag = 0;
            for (int i = 1; i <= n; i++)
            {
                int nw = ord[i];
                if (check(nw)) //判断这个点能否进行合并
                {
                    flag = 1;
                    int f = find(rod[nw][0]);
                    bel[nw].first = f;
                    bel[f].second += bel[nw].second;
                    ans=max(bel[f].second,ans);
                }
            }
            if (!flag) //如果所有点都不能进行合并，结束
                break;
        }
        // for (int i = 1; i <= n; i++)
        //     ans = max(ans, bel[i].second);
        printf("Case #%d: %d\n", tt++, ans);
    }
    return 0;
}
//参考https://ac.nowcoder.com/acm/contest/view-submission?submissionId=52793209

ED

  1. 该学数学了，不然H补不了；
  2. 这场题解不太好写，也许和我太长时间没写题解有关系；
  3. 14159；
算法竞赛 > 比赛与题集
2022牛客暑期多校训练营1（ACDGIJ）
https://tanyuu.github.io/2022.07-12/2022牛客暑期多校训练营1（ACDGIJ）/
作者
F Juny
发布于
2022年7月22日
许可协议