NEFU大一暑假集训-并查集

题集链接

OP

感谢ph和zsl两位大佬的指导与讨论；

A 食物链

思路

查看PDF即可~
两种做法，下面代码中选择了扩展域；

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
#include <stdio.h>
#include<iostream>
using namespace std;
typedef long long ll;
int fa[150004];
int find(int x)
{
    if (fa[x] == x)
        return x;
    else
        return find(fa[x]);
}
int main()
{
    int n, k, ans = 0, o, a, b, i;
    cin >> n >> k;
    for (i = 1; i <= 3 * n; i++)
        fa[i] = i;
    while (k--)
    {
        scanf("%d%d%d", &o, &a, &b);
        if (a > n || b > n)
        {
            ans++;
            continue;
        }
        if (o == 1) //同类
        {
            if (find(a + n) == find(b) || find(a + 2 * n) == find(b))
                ans++;
            else
            {
                fa[find(a)] = find(b);
                fa[find(a + n)] = find(b + n);
                fa[find(a + 2 * n)] = find(b + 2 * n);
                //按同类维护
            }
        }
        else if (o == 2) //a吃b
        {
            if (find(a) == find(b) || find(a) == find(b + n))
                ans++;
            else
            {
                fa[find(a + n)] = find(b);
                fa[find(a + 2 * n)] = find(b + n);
                fa[find(a)] = find(b + 2 * n);
            }
        }
    }
    cout << ans;
}

B 关押罪犯

思路

详见PDF~；

贪心，优先分配矛盾最严重的，直到无法分配；

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
#include <stdio.h>
#include <iostream>
#include <algorithm>
using namespace std;
typedef long long ll;
const ll N = 100005;
int fa[N] = {0};
struct dat
{
    int a, b, c;
} da[N];
bool cmp(dat a, dat b)
{
    return a.c > b.c;
}
int find(int x)
{
    return fa[x] == x ? x : fa[x] = find(fa[x]);
}
int main()
{
    int n, m, i;
    cin >> n >> m;
    for (i = 1; i <= m; i++)
        scanf("%d%d%d", &da[i].a, &da[i].b, &da[i].c);
    sort(da + 1, da + 1 + m, cmp);
    for (i = 1; i <= 2 * n; i++)
        fa[i] = i;           //初始化
    for (i = 1; i <= m; i++) //贪心，从大到小找到第一个发生冲突的
    {
        if (find(da[i].a) == find(da[i].b)) //存在冲突
        {
            printf("%d", da[i].c);
            return 0;
        }
        else
        {
            fa[find(da[i].a)] = find(da[i].b + n);
            fa[find(da[i].b)] = find(da[i].a + n);
            //把一个加入另一个的扩展域，代表放入相异的集合
        }
    }
    printf("0");
    return 0;
}

C 程序自动分析

思路

详见PDF~；

先把要求相同的放在同一集合中，再查看要求不同的是否有冲突；

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
#include <stdio.h>
#include <iostream>
#include <algorithm>
#include <map>
using namespace std;
typedef long long ll;
int fa[200005]; //fa数组
pair<int, int> e0[200005];
//存储需要不同值的数对，统一判冲
map<int, int> mp; //映射表
int c, ce0;
int find(int x)
{
    if (fa[x] == x)
        return x;
    return fa[x] = find(fa[x]);
}
int main()
{
    int t, n, a, b, e;
    cin >> t;
    while (t--)
    {
        mp.clear();
        c = 1, ce0 = 0; //初始化
        scanf("%d", &n);
        int f = 1;
        for (int i = 1; i <= 200000; i++) //初始化
        {
            fa[i] = i;
        }
        for (int i = 1; i <= n; i++)
        {
            scanf("%d%d%d", &a, &b, &e);
            if (!mp[a])
                mp[a] = c++;
            if (!mp[b])
                mp[b] = c++;
            //若值不存在，则为其分配哈希值
            a = mp[a], b = mp[b];
            if (!e)
            {
                e0[ce0++] = {a, b};
            }
            else
            {
                fa[find(a)] = find(b); //合并
            }
        }
        for (int i = 0; i < ce0 && f; i++) //处理需要不同值的值对
        {
            if (find(e0[i].first) == find(e0[i].second))
                f = 0;
        }
        if (f)
            printf("YES\n");
        else
            printf("NO\n");
    }
    return 0;
}

D 最小生成树

思路

最小生成树板题~

这里是直接用天空之城代码改的；

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
int fa[200005], cnt[200005];
ll len[200005];
struct road
{
    int fr, to;
    ll lrd;
} rod[500005];
bool cmp(road a, road b)
{
    return a.lrd < b.lrd;
}
int find(int x)
{
    if (fa[x] != x)
        fa[x] = find(fa[x]);
    return fa[x];
}
int main()
{
    int n, q, i;
    while (~scanf("%d%d", &n, &q))
    {
        int g1,g2,glen;
        for (i = 1; i <= q; i++)
        {
            cin >> g1;
            cin >> g2;
            scanf("%d", &glen);
            rod[i].fr = g2, rod[i].to = g1, rod[i].lrd = glen; //存路
        }
        sort(rod + 1, rod + 1 + q, cmp);
        for (i = 1; i <= n; i++)
            fa[i] = i, cnt[i] = 1, len[i] = 0; //初始化并查集
        for (i = 1; i <= q; i++)
        {
            int frn = rod[i].fr, ton = rod[i].to;
            if (find(frn) != find(ton))
            {
                if (find(frn) > find(ton))
                    swap(frn, ton);
                cnt[find(frn)] += cnt[find(ton)];
                len[find(frn)] += len[find(ton)] + rod[i].lrd;
                fa[find(ton)] = find(frn);
            }
        }
        if (cnt[1] == n)
            printf("%lld\n", len[1]);
        /* else
            printf("No!\n"); */
    }
    return 0;
}

E Lomsat gelral

按秩合并思想

题目大意

给出树状结构和每个节点的颜色编号，输出以每个节点为根的子树出现次数最多的若干颜色编号之和；

思路

在dfs搜索时，对某节点下每个子树的颜色需要单独维护，如果对每一子树都重复进行维护和撤销，显然在处理以该节点为根的子树时又需要把这些子树再维护；
我们可以保留权重最大的子树，最后处理，处理后再维护其他子树的值，直接作为以该节点为根的整个子树的颜色统计；

对于颜色统计，我们可以用桶来维护，在搜索最大颜色时不必扫描整个桶数组，以子树的根节点进行dfs即可；

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
#include <iostream>
#include <algorithm>
#include <string.h>
#include <math.h>
#include <map>
#include <vector>
using namespace std;

const int N = 1e5 + 10;

vector<int> E[N];
int col[N];
long long ans[N];
int tmp[N];
bool is[N];
int sz[N];
long long mxtmp, astmp;

void get_inf(int u, int fa = -1)
{
    int it;
    int maxx = -1;
    for (auto t : E[u])
    {
        if (t == fa)
            continue;
        get_inf(t, u);
        sz[u] += sz[t];
        if (sz[t] > maxx)
        {
            maxx = sz[t];
            it = t;
        }
    }
    if (maxx != -1)
        is[it] = true;
}

void clear(int u, int fa = -1)
{
    tmp[col[u]]--;
    for (auto t : E[u])
    {
        if (t == fa)
            continue;
        clear(t, u);
    }
}

void get_ans(int u, int fa, int p = -1)
{
    tmp[col[u]]++;
    if (tmp[col[u]] > mxtmp)
    {
        mxtmp = tmp[col[u]];
        astmp = col[u];
    }
    else if (tmp[col[u]] == mxtmp)
    {
        astmp += col[u];
    }
    for (auto t : E[u])
    {
        if (t == fa || t == p)
            continue;
        get_ans(t, u);
    }
}

void dfs(int u, int fa = -1)
{
    int p = 0;
    for (auto t : E[u])
    {
        if (t == fa)
            continue;
        if (is[t])
        {
            p = t;
            continue;
        }
        dfs(t, u);
        clear(t, u);
        mxtmp = astmp = 0;
    }
    if (p)
        dfs(p, u);
    get_ans(u, fa, p);
    ans[u] = astmp;
}

int main()
{
    int n;
    cin >> n;
    for (int i = 1; i <= n; i++)
        scanf("%d", &col[i]), sz[i] = 1;
    for (int i = 1, u, v; i < n; i++)
    {
        scanf("%d%d", &u, &v);
        E[u].push_back(v);
        E[v].push_back(u);
    }
    get_inf(1);
    dfs(1);
    for (int i = 1; i <= n; i++)
        printf("%lld ", ans[i]);
    return 0;
}

F 修复公路

思路

最小生成树~

只不过这里求的是生成树中最大边权；

同样改自天空之城；

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
int fa[200005], cnt[200005]; //fa存该城所在集合的根节点（城市），cnt存以该城为根的集合城市数
ll len[200005]; //len存以该城为根的集合内部的连通代价
struct road
{
    int fr, to;
    ll lrd;
} rod[500005];
bool cmp(road a, road b)
{
    return a.lrd < b.lrd;
}
int find(int x)
{
    if (fa[x] != x)
        fa[x] = find(fa[x]);
    return fa[x];
}
int main()
{
    int n, q, i;
    while (~scanf("%d%d", &n, &q))
    {
        int g1,g2,glen;
        for (i = 1; i <= q; i++)
        {
            cin >> g1;
            cin >> g2;
            scanf("%d", &glen);
            rod[i].fr = g2, rod[i].to = g1, rod[i].lrd = glen; //存路
        }
        sort(rod + 1, rod + 1 + q, cmp);
        for (i = 1; i <= n; i++)
            fa[i] = i, cnt[i] = 1, len[i] = 0; //初始化并查集
        for (i = 1; i <= q; i++)
        {
            int frn = rod[i].fr, ton = rod[i].to;
            if (find(frn) != find(ton))
            {
                if (find(frn) > find(ton))
                    swap(frn, ton);
                cnt[find(frn)] += cnt[find(ton)];
                len[find(frn)] = max(len[find(ton)] , rod[i].lrd); //处理连通代价
                fa[find(ton)] = find(frn);
            }
        }
        if (cnt[1] == n)
            printf("%lld\n", len[1]);
        else
            printf("-1\n"); 
    }
    return 0;
}

G 奶酪

思路

这里用的是BFS；

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
#include <queue>
#include <stdio.h>
#include <iostream>
#include <string.h>
using namespace std;
typedef long long ll;

struct ball
{
    double x,y,z;
} bll[1003];
int n;
double h,r;
bool gt[1003];
queue<int>que;

bool dis(int i,int j)
{
    return (bll[i].x-bll[j].x)*(bll[i].x-bll[j].x)+
            (bll[i].y-bll[j].y)*(bll[i].y-bll[j].y)+
             (bll[i].z-bll[j].z)*(bll[i].z-bll[j].z)<=4*r*r;
}

bool bfs()
{
    int f=0;
    while(!que.empty())
    {
        int now=que.front();
        if(h-bll[now].z<=r)
        {
            f=1;
            break;
        }
        que.pop();
        for(int i=1;i<=n;i++)
        {
            if(!gt[i]&&dis(i,now))
            {
                gt[i]=1;
                que.push(i);
            }
        }
    }
    if(f)
    {
        while(!que.empty())que.pop();
    }
    return f;
}

int main()
{
    int t;
    cin>>t;
    while(t--)
    {
        memset(gt,0,sizeof gt);
        scanf("%d%lf%lf",&n,&h,&r);
        for(int i=1;i<=n;i++)
        {
            scanf("%lf%lf%lf",&bll[i].x,&bll[i].y,&bll[i].z);
            if(bll[i].z<=r)
            {
                gt[i]=1;
                que.push(i);
            }
        }
        if(bfs())printf("Yes\n");
        else printf("No\n");
    }
    return 0;
}

I City

题目大意

给出城市，道路和道路强度，求问在不同强度的攻击下，有多少城市对之间仍有通路；

思路

显然，若对于每一次攻击重新进行搜索是不实际的；

由于高强度攻击下剩余的道路一定是低强度攻击下剩余道路的子集，所以我们可以从高到低处理询问，逐步添加道路；

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
#include <queue>
#include <stdio.h>
#include <iostream>
#include <string.h>
#include <algorithm>
using namespace std;
typedef long long ll;

struct road
{
    int a,b,z;
} rod[200005];
pair<pair<int,int> ,ll>tt[200005];
int fa[200005];
ll cnt[200005];
bool cmpr(road A,road B)
{
    return A.z>B.z;
}
bool cmpt(pair<pair<int,int> ,ll> A,pair<pair<int,int> ,ll> B)
{
    return A.first.second>B.first.second;
}
bool cmptt(pair<pair<int,int> ,ll> A,pair<pair<int,int> ,ll> B)
{
    return A.first.first<B.first.first;
}
int find(int x)
{
    return fa[x]==x?x:fa[x]=find(fa[x]);
}
int main()
{
    int t;
    cin>>t;
    while(t--)
    {
        int n,m,q;
        scanf("%d%d%d",&n,&m,&q);
        for(int i=1;i<=m;i++)
        {
            scanf("%d%d%d",&rod[i].a,&rod[i].b,&rod[i].z);
        }
        for(int i=1;i<=q;i++)
        {
            scanf("%d",&tt[i].first.second);
            tt[i].first.first=i;
        }
        sort(rod+1,rod+1+m,cmpr);
        sort(tt+1,tt+1+q,cmpt);
        for(int i=1;i<=n;i++)
        {
            fa[i]=i;
            cnt[i]=1;
        }
        int j=1;
        ll ans=0;
        for(int i=1;i<=q;i++)
        {
            //if(rod[j].z>=tt[i].first.second)
            for(j;rod[j].z>=tt[i].first.second;j++)
            {
                int faa=find(rod[j].a),fab=find(rod[j].b);
                if(faa!=fab)
                {
                    ans+=cnt[faa]*cnt[fab];
                    fa[faa]=fab;
                    cnt[fab]+=cnt[faa];
                }
            }
            tt[i].second=ans;
        }
        sort(tt+1,tt+1+q,cmptt);
        for(int i=1;i<=q;i++)
        {
            printf("%lld\n",tt[i].second);
        }
    }
    return 0;
}

J The Child and Zoo

“最大生成树”

题目大意

给定每一个节点的权重和网状结构，定义f(i,j)f(i,j)为 i 到 j 的所有简单路径中，途径节点最小值的最大值；
求
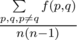
在这里插入图片描述

思路

对于每条道路，道路的权值即可认为是道路两端节点权值的最小值；

从大到小排列所有道路，生成“最大生成树”，对于每次连接操作，即可认为道路一段所在区块与另一端所在区块的元素两两之间的 f 值均为此道路的权值；

代码

代码依然修改自天空之城；

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
#include <iostream>
#include <algorithm>
#include <string.h>
#include <math.h>
#include <map>
#include <vector>
using namespace std;
typedef long long ll;
int fa[200005], cnt[200005],qu[200005];
ll len[200005];              //len存以该城为根的集合内部的连通代价
struct road
{
    int fr, to;
    ll lrd;
} rod[500005];
bool cmp(road a, road b)
{
    return a.lrd > b.lrd;
}
int find(int x)
{
    if (fa[x] != x)
        fa[x] = find(fa[x]);
    return fa[x];
}
int main()
{
    int n, q, i;
    scanf("%d%d", &n, &q);
    for(int i=1;i<=n;i++)scanf("%d",&qu[i]);
    int g1, g2, glen;
    for (i = 1; i <= q; i++)
    {
        cin >> g1;
        cin >> g2;
        //scanf("%d", &glen);
        rod[i].fr = g2, rod[i].to = g1, rod[i].lrd = min(qu[g1],qu[g2]); //存路
    }
    sort(rod + 1, rod + 1 + q, cmp);
    for (i = 1; i <= n; i++)
        fa[i] = i, cnt[i] = 1, len[i] = 0; //初始化并查集
    ll ans=0;
    for (i = 1; i <= q; i++)
    {
        int frn = rod[i].fr, ton = rod[i].to;
        if (find(frn) != find(ton))
        {
            if (find(frn) > find(ton))
                swap(frn, ton);
            ans+=(ll)rod[i].lrd*cnt[find(frn)]*cnt[find(ton)];
            cnt[find(frn)] += cnt[find(ton)];
            len[find(frn)] += len[find(ton)] + rod[i].lrd;
            fa[find(ton)] = find(frn);
        }
    }
    printf("%.6lf\n", 1.0*ans/(1.0*n*(n-1)/2));

    return 0;
}

ED

\

算法竞赛 > 比赛与题集
NEFU大一暑假集训-并查集
https://tanyuu.github.io/2021.07-12/NEFU大一暑假集训-并查集（ABCDEFGIJ）/
作者
F Juny
发布于
2021年8月16日
许可协议