NEFU大一暑假集训-前缀和与差分（LMRSTUVXYZ）

OP

感谢老师的讲解与付出；
感谢ph和zsl两位大佬的指导与讨论；

题量好大XD；

~~如果用甲子命名法就可以出60道了；~~

总的来说，对于一个数组 $a_i$ ，其与其差分数组 $d_i$ 和前缀和数组 $s_i$ 存在以下关系：（边界条件未仔细调整）

a_n=\sum_{i=1}^nd_i $$$$s_n=\sum_{i=1}^n a_i$$通过此规律，我们便可以在线性复杂度内完成从差分数组（$O(1)$ 区间修改）到前缀和数组（$O(1)$ 区间查询）之间的转换； ## L 子段求和板，处理出前缀和后，作差出子段和即可； #### 题目大意给出一个长度为N的数组，进行Q次查询，查询从第i个元素开始长度为l的子段所有元素之和。 #### 代码

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
ll s[50004];
int main()
{
    int n,g,a,b;
    cin>>n;
    for(int i=1;i<=n;i++)
        cin>>g,s[i]=s[i-1]+g;
    cin>>g;
    while(g--)
    {
        cin>>a>>b;
        printf("%lld\n",s[a+b-1]-s[a-1]);
    }
    return 0;
}

## M Alyona and a tree [参考](https://blog.csdn.net/qq_34374664/article/details/70246427) #### 题目大意给出一棵根树，每个节点上和每一条边上都标记有一个正整数；定义 $dist(v, u)$ ：为从 v 到 u 的简单路径中，边上的正整数之和；定义 v 控制 u （$u\not=v$）：u 在 v 的子树中，并且 $dist(v, u) \leqslant a_u$ ；**a~u~！！！** 输出每一个节点所能控制的节点个数； #### 思路对于某节点 $u_n$，在从根节点到该节点的路径 $u_1,u_2,...,u_n$ 中，如果 $u_{i}$ 不能对 $u_n$ 产生控制，则所有 $u_j(j\leqslant i)$ 均不能对其产生控制，此规律满足了二端性（以二分）和前缀性质（以前缀统计）; 所以我们可以在对树dfs的同时，对 $u_n$ 维护好路径 $u_1,u_2,...,u_n$ 上的 $dist(u_1,u_1),dist(u_1,u_2),...,dist(u_1,u_n)$ ；此时有 $dist(u_i,u_n)=dist(u_1,u_n)-dist(u_1,u_{i-1})$ ，我们可以通过二分确定最前一个能对 $u_n$ 产生控制的点；在统计部份，我们可以认为对于节点 $u_i$ ，其“本应”控制其子节点控制的所有点，但是子树中有一些点 $u_j$ ，最远能控制其的点是 $u_i$ 的子节点，那么在统计 $u_i$ 的控制数时应把他们减去，并在统计上级节点时同样不计入；此时便应用了差分思想，在二分出最前一个能对 $u_j$ 产生控制的点时，应该在对应的位置标记 -1，即为控制数-1，在统计中便减掉了此点； #### 代码

#include <stdio.h>
#include <iostream>
#include <math.h>
#include <queue>
#include <cstring>
#include <algorithm>
using namespace std;
typedef long long ll;
const int MAXN = 2e5 + 5;
vector<pair<ll, int>> G[MAXN], path;
ll dep[MAXN];
int sum[MAXN], a[MAXN];

void dfs(int u)
{
    path.push_back(make_pair(dep[u], u));
    int it = lower_bound(path.begin(), path.end(), make_pair(dep[u] - a[u], -1)) - path.begin() - 1;
    if (it >= 0)
        sum[path[it].second]--;
    for (int i = 0; i < G[u].size(); i++)
    {
        int v = G[u][i].first, w = G[u][i].second;
        dep[v] = dep[u] + w;
        dfs(v);
        sum[u] += sum[v] + 1;
    }
    path.pop_back();
}

int main()
{
    memset(sum, 0, sizeof(sum));
    int n;
    cin >> n;
    int t, w;
    for (int i = 1; i <= n; i++)
        scanf("%d", &a[i]);
    for (int i = 2; i <= n; i++)
    {
        scanf("%d%d", &t, &w);
        G[t].push_back(make_pair(i, w));
    }
    dep[1] = 0;
    dfs(1);
    for (int i = 1; i <= n; i++)
        printf("%d ", sum[i]);
    return 0;
}

## R 前缀和板，处理出前缀和后，输出即可； #### 题目大意输入一个长度为n(1 <= n <= 100000)数组ai(0<=ai<=1000)，输出他的前缀和。 #### 代码

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
ll s[100005];
int ans=0;
int main()
{
    int n,g,a,b;
    cin>>n;
    for(int i=1;i<=n;i++)
        cin>>g,s[i]=s[i-1]+g;
    printf("%d\n",n);
    for(int a=1;a<=n;a++){
        printf("%lld\n",s[a]);
    }
    return 0;
}

## S 校门外的树 #### 题目大意 >某校大门外长度为L的马路上有一排树，每两棵相邻的树之间的间隔都是 1 米。我们可以把马路看成一个数轴，马路的一端在数轴 0 的位置，另一端在 L 的位置；数轴上的每个整数点，即 0，1，2，⋯，L ，都种有一棵树。由于马路上有一些区域要用来建地铁。这些区域用它们在数轴上的起始点和终止点表示。已知任一区域的起始点和终止点的坐标都是整数，区域之间可能有重合的部分。现在要把这些区域中的树（包括区域端点处的两棵树）移走。你的任务是计算将这些树都移走后，马路上还有多少棵树。 #### 思路像扫雪那道题，对于每一个砍树的区间，我只需要在区间左端点标记+1，右端点标记-1，之后扫一遍差分数组并累加差分值，统计有多少个位置累加值为0即可； #### 代码

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
ll s[100005];
int ans=0;
int main()
{
    int n,t;
    cin>>n>>t;
    n++;
    int a,b;
    while(t--)
    {
        cin>>a>>b;
        a++,b++;
        s[a-1]++;
        s[b]--;
    }
    int m=s[0];
    for(int i=1;i<=n;i++)
    {
        if(!m)ans++;
        m+=s[i];
    }
    cout<<ans;
    return 0;
}

## T 激光炸弹 #### 题目大意给出每一个目标的坐标与价值，求任意 $R\times R$ 范围内总价值的最大值 #### 思路数据量不大，二位前缀和处理后，穷举每个点，算出以其为左下点 / 右上点的 $R\times R$ 区间内的价值和； #### 代码

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
int s[5003][5003];
int ans=0;
int main()
{
    int n,r;
    cin>>n>>r;
    int x,y,v;
    while(n--)
    {
        cin>>x>>y>>v;
        x++,y++;
        s[x][y]=v;
    }
    for(int i=1;i<=5001;i++)
    for(int j=1;j<=5001;j++)
    s[i][j]+=s[i-1][j]+s[i][j-1]-s[i-1][j-1];
    for(int i=r;i<=5001;i++)
    {
        for(int j=r;j<=5001;j++)
        {
            ans=max(ans,s[i][j]-s[i-r][j]-s[i][j-r]+s[i-r][j-r]);
        }
    }
    cout<<ans;
    return 0;
}

## U 天上的星星 #### 题目大意给出每一个星星的坐标与亮度，求任意给定范围内的亮度和； #### 思路二位前缀和处理后，输出给定范围的和即可 #### 代码

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
ll s[2003][2003];
int ans=0;
//int k,row[2003],col[2003];
int main()
{
    int n;
    cin>>n;
    int x,y,v;
    while(n--)
    {
        cin>>x>>y>>v;
        x++,y++;
        s[x][y]+=v;
    }
    for(int i=1;i<=2001;i++)
    for(int j=1;j<=2001;j++)
    s[i][j]+=s[i-1][j]+s[i][j-1]-s[i-1][j-1];
    int q,x1,x2,y1,y2;
    cin>>q;
    while(q--)
    {
        cin>>x1>>y1>>x2>>y2;
        x1++,x2++,y1++,y2++;
        printf("%lld\n",s[x2][y2]-s[x2][y1-1]-s[x1-1][y2]+s[x1-1][y1-1]);
    }
    return 0;
}

## V 程序设计：蒜头君的数轴 [参考](https://blog.csdn.net/weixin_43154720) #### 题目大意给定数轴上的一些点，要求添加一些点，使相邻两点的距离最多有一个和其余不相等，求出添加的最少点数； #### 思路显然，如果要求所有间隔相等，我们需要求出所有区间长度的gcd，并用每个区间长度去除，累加获取答案；在此题的条件中，所有区间长度的gcd就变为**除一个区间外**其他区间长度的gcd最大值；为求解这个值，我们可以算出每一位的前缀gcd和后缀gcd，并枚举扣掉每个区间，算出其余区间的gcd，并取最大值； #### 代码

#include <stdio.h>
#include <iostream>
#include <math.h>
#include <queue>
#include <cstring>
#include <algorithm>
using namespace std;
typedef long long ll;
const int maxn = 100005;
int a[maxn];
int l[maxn], r[maxn], pre[maxn];
int main()
{
    int n;
    scanf("%d", &n);
    for (int i = 0; i < n; i++)
        scanf("%d", &a[i]);
    sort(a, a + n);
    int sum = 0;
    for (int i = 1; i < n; i++)
        pre[i - 1] = a[i] - a[i - 1];
    l[0] = pre[0]; //初始化前后缀gcd
    r[n - 1] = pre[n - 1];
    for (int i = 1; i < n; i++) ///从前往后求DCD
        l[i] = __gcd(l[i - 1], pre[i]);
    for (int i = n - 2; i >= 0; i--) ///从后往前求GCD
        r[i] = __gcd(r[i + 1], pre[i]);
    int mx = 0;
    int pos = 0;
    for (int i = 0; i < n; i++)//枚举跳过每个区间
    {
        int te = __gcd(l[i - 1], r[i + 1]);//之前的前缀gcd与之后的后缀gcd
        if (te >= mx) ///找跳过某区间的最大公因数
        {
            mx = te;
            pos = i;
        }
    }
    for (int i = 0; i < n - 1; i++)
    {
        if (i != pos)
            sum += pre[i] / mx - 1; ///每一段需要添加多少个点
    }
    cout << sum << endl;
    return 0;
}

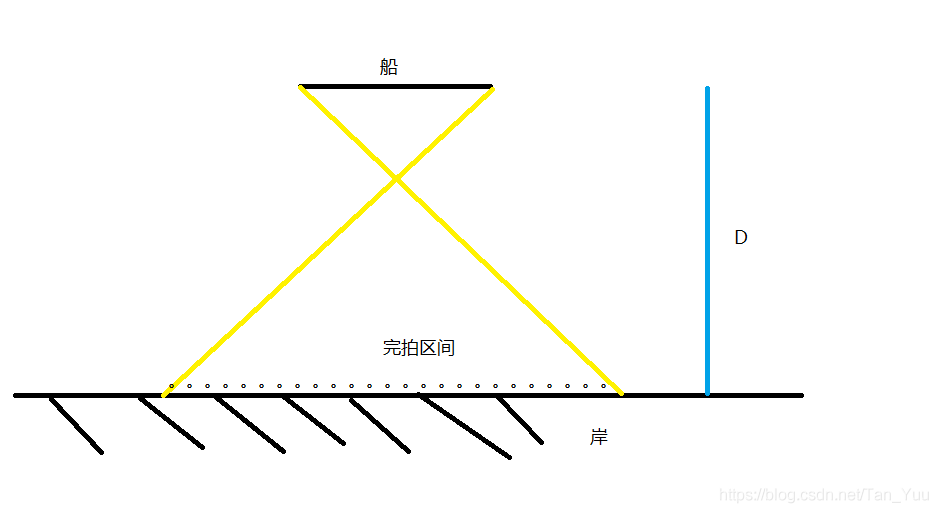
## X 拍照 #### 题目大意太复杂了，略 #### 思路我们将两个方向运动的船拆开来看：对于每艘船，已知其左右坐标和距岸距离，其**在岸上能够完整被拍摄的位置区间**（后称完拍区间）是确定的； ![在这里插入图片描述](https://s2.loli.net/2022/08/02/hQO7YdZBxqXHGf5.png) 对于同方向的所有船，每个船对应的完拍区间的相对位置不会改变，也就是说，对于初始时刻的某个方向，岸边每个点都会拍到一定数量的船（后将这个序列成为船数序列）；具体统计操作可以用差分数组实现；对于岸边的某个点，随着时间的流逝，它可以拍到右行船的船数序列中，此点左侧的任意值（船同时向右开）；同理，也可以拍到左行船的船数序列中，此点右侧的任意值；如果要求最大值，我们只需要维护右行船的前缀最大值和左行船的后缀最大值，并找出两个最大值之和的最大值即可； #### 代码 1. 注意防负 2. 比较卡时间，下面的 $2.02e6$ 如果改成 $5e6$ 就会TLE

#include <stdio.h>
#include <iostream>
#include <math.h>
#include <queue>
#include <cstring>
using namespace std;
typedef long long ll;
int to[2][2020006];//to[0] is to left
int main()
{
    int t,n,x,y,z,d,zzz=0;
    cin>>t;
    while(t--)
    {        
        zzz++;
        memset(to,0,sizeof to);
        cin>>n;
        while(n--)
        {
            scanf("%d%d%d%d",&x,&y,&z,&d);
            //cin>>x>>y>>z>>d;
            if(d==-1)d=0;
            x+=z;
            y-=z;
            x+=1010000;
            y+=1010000;
            if(x<y)continue;//如果完拍区间不存在
            to[d][y]++;
            to[d][x+1]--;
        }
        int sum[2]={0};
        for(int i=1;i<=2020000;i++)
        {
            for(int j=0;j<2;j++) //船数序列去差分
            {
                sum[j]+=to[j][i];
                to[j][i]=sum[j];
            }
            to[1][i]=max(to[1][i-1],to[1][i]);//前缀最大值
        }
        for(int i=2020000;i>=1;i--)//后缀最大值
        {
            to[0][i]=max(to[0][i+1],to[0][i]);
        }
        int ma=-1;
        for(int i=1;i<=2020000;i++)
        {
            ma=max(ma,to[0][i]+to[1][i]);
        }
        printf("Case #%d:\n%d\n",zzz,ma);
    }
}

## Y Saitama Destroys Hotel #### 题目大意电梯很特别——它从顶层开始，只能向下移动，容量无限。楼层从0到s编号，电梯最初在时间0时从楼层s启动。电梯只需要1秒钟就可以准确地向下移动1层，而接客的时间可以忽略不计。Genos 会收到一份详细说明乘客到达的时间和楼层的列表。请确定 Genos 将所有乘客带到0层需要多长时间（以秒为单位）。 #### 思路存储每层最后一位乘客的到达时间，模拟即可~ 注意边界； #### 代码

#include <stdio.h>
#include <iostream>
#include <math.h>
#include <queue>
using namespace std;
typedef long long ll;
int a[1003];
int main()
{
    int n,s;
    int b,c;
    cin>>n>>s;
    for(int i=1;i<=n;i++)
    {
        cin>>b>>c;
        if(a[b])a[b]=max(a[b],c);
        else a[b]=c;
    }
    int t=-1;
    for(int i=s;i>=0;i--)
    {
        t++;
        t=max(t,a[i]);
    }
    cout<<t;
}

## Z Greg and Array #### 题目大意对于给定数组和给定操作（左界，右界，增加值），给出 k 次变动，每次变动给出**操作的编号区间**（而不是被操作数组元素的编号区间），输出最后数组的结果； #### 思路将数组先转换为差分数组，方便操作；记录每个操作的编号和操作内容；再接收k次变动，通过差分记录每个操作的操作次数；再在数组中执行这些操作；再复原数组，并输出； #### 代码

#include <stdio.h>
#include <iostream>
#include <math.h>
#include <queue>
using namespace std;
typedef long long ll;
ll a[100005],o[100005];
pair<pair<int,int>,int>opt[100005];
int main()
{
    int n,m,k,g;
    cin>>n>>m>>k;
    for(int i=1;i<=n;i++)//差分化
    {
        cin>>g;
        a[i]+=g;
        a[i+1]-=g;
    }
    int l,r,d;
    for(int i=1;i<=m;i++)//接收操作并记录
    {
        cin>>opt[i].first.first>>opt[i].first.second>>opt[i].second;
    }
    for(int i=1;i<=k;i++)//接收改动，并差分存储每个操作的操作数
    {
        cin>>l>>r;
        o[l]++;
        o[r+1]--;
    }
    ll sum=0;
    for(int i=1;i<=m;i++)//遍历所有操作，统计操作数，操作
    {
        sum+=o[i];
        if(sum){
        a[opt[i].first.first]+=opt[i].second*sum;
        a[opt[i].first.second+1]-=opt[i].second*sum;
        }
    }
    a[0]=0;
    for(int i=1;i<=n;i++)//还原数组并输出
    {
        a[i]+=a[i-1];
        printf("%lld",a[i]);
        if(i!=n)printf(" ");
    }
}

## ED 比较赶，如有疏漏，敬请提出

算法竞赛 > 比赛与题集

NEFU大一暑假集训-前缀和与差分（LMRSTUVXYZ）

https://tanyuu.github.io/2021.07-12/NEFU大一暑假集训-前缀和与差分（LMRSTUVXYZ）/

作者

F Juny

发布于

2021年7月24日

许可协议

NEFU大一暑假集训-Hash（ABCDEH）上一篇

NEFU大一暑假集训-尺取法下一篇