2021牛客寒假算法基础集训营1（A B C D E F H I J）

比赛链接：这里

OP

个人能力有限，有的题目实在知识点欠缺太多，可以参照一下其他大佬的全题解。
&感谢ph大佬的全程指导。

A 串

递推。

思路

我们可以先算出长度为 1,2,…,n 的合法串的数量，再进行累加。

介于数据量（2 < n <= 106)，通过排列组合来求几乎不可能，单纯打表可能就需要几十分钟。

接下来就是具体的递推过程：

假设长度为 n 的合法字符串有 An 个。长度为 n + 1 的字符串中的前 n 项可以分为两种情况：合法的与非法的。

——对于前 n 项为合法字符串的 n + 1 长字符串，显然情况有 An * 26 种（即第 n + 1 项可以为任意字母）；
——对于前 n 项为非法字符串的 n + 1 长字符串，只有前 n 项存在 u 的字符串可以变为合法串，所以含 u 的 n 长字符串的数量为 26n - 25n 个，其中有 An 个合法串，所以此种情况的 n + 1 长合法串有 26n - 25n - An 个（即存在 u 的 n 长非法字符串数量为 含 u 的 n 长字符串数量 减去 合法的 n 长字符串数量，该种串后接 s 即变为合法串）。

所以得到递推公式 An+1 = 25 * An + 26n - 25n

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
#include <bits/stdc++.h>
using namespace std;
const long long MOD = 1e9 + 7;
long long qs(long long a,long long t)//快速幂取模
{
    long long ans=1;
    while(t)
    {
        if(t&1)ans=ans*a%MOD;
        a=a*a%MOD;
        t>>=1;
    }
    return ans%MOD;
}
int main()
{
    long long a=1,i,j,n,ans=1;cin>>n;
    for(i=3;i<=n;i++)
    {
        a=a*25+qs(26,i-1)-qs(25,i-1);
        a%=MOD;
        if(a<0)a+=MOD;
        ans+=a;//累加
        ans%=MOD;
    }
    printf("%lld",ans);
    return 0;
}

B 括号

此题为特判题（Special Judge）

思路

首先我们观察样例，即可得知总括号对数为 每一个左括号后面的右括号总数的累加和。

所以说，为使总字符量尽可能少，我们需要把 k 先粗略地拆成 l1 * r1 的形式（ l1 * r1 <= k ）， l1 与 r1 需要尽可能接近（均值不等式）；

我们可以取 l1 = ⌊ sqrt( k ) ⌋，则 r1 = ⌊ k / l1 ⌋，此时还需要补上差值 d = k - l1 * r1 ；

接下来就是构造了：我们可以依次输出 l1 个左括号，r1 - d 个右括号，1 个左括号，d 个右括号。此时总对数则为 l1 * r1 + d 。

要求是非空串，注意对 0 特判。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
#include <bits/stdc++.h>
using namespace std;

int main()
{
    int k,l,r,d,i;
    scanf("%d",&k);
    if(k==0){printf("(");return 0;}
    l=(int)sqrt(k);
    r=k/l;
    d=k-r*l;
    for(i=1;i<=l;i++)printf("(");
    for(i=1;i<=r-d;i++)printf(")");
    printf("(");
    for(i=1;i<=d;i++)printf(")");
    return 0;
}

比赛时使用的另一种方法，即把 k 拆成 n1 * a12 + n1 * a12 + … 的形式，再构造输出，代码如下，可ac，仅做参考。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
#include <bits/stdc++.h>
using namespace std;

int main()
{
    int k,i,ma,j;
    scanf("%d",&k);
    if(k==0){printf("(");return 0;}
    int a[31623]={0};
    ma=(int)sqrt(k);
    while(k)
    {
        a[(int)sqrt(k)]++;
        k-=(int)sqrt(k)*(int)sqrt(k);
    }
    for(i=1;i<=ma;i++)
    {
        printf("(");
        if(a[i])
        {
            for(j=1;j<=i*a[i];j++)printf(")");
        }
    }
    return 0;
}

C 红和蓝

dfs，涂色

思路

使用两遍bfs，第一遍进行分组和可行性判定，第二遍进行染色

具体实现上（也可以使用链表存图）：

第一次dfs时，先递归处理下级节点，再将其与上级节点分入同一组，同时完成可行性判定；

第二次dfs时，判断其与上级节点是否在同一组，在即涂与上级相同的颜色，不在即将自己涂成与上级不同的颜色；

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
#include <bits/stdc++.h>
using namespace std;
const int N = 2e5 + 5;
struct node{
    int to, next;
}edge[N];
int head[N], cnt;//cnt为道路数组序号
int mrk[N], col[N], num;//num计组数
bool flag;

void add(int u, int v)
{
    edge[++cnt] = {v, head[u]};//标记前向标
    head[u] = cnt;//更新待标记前向标
}

void dfs1(int u, int fa)
{
    int son = 0;
    for(int i = head[u]; i != -1; i = edge[i].next)
    {
        int v = edge[i].to;
        if(v != fa)
        {
        	son++;
        	dfs1(v, u);
        }
    }
    if(son == 0 || mrk[u] == 0)//叶节点与未被下级节点涂色的节点需被涂色
    {
        if(mrk[fa] != 0)//如果其上级节点已被涂色
        {
            flag = 0;
            return ;
        }
        mrk[u] = mrk[fa] = ++num;//此节点与上级节点标成同一数字
    }
}

void dfs2(int u, int fa)
{
    for(int i = head[u]; i != -1; i = edge[i].next)
    {
        int v = edge[i].to;
        if(v == fa) continue;
        if(mrk[v] == mrk[u])//同组即同色
            col[v] = col[u];
        else col[v] = !col[u];//异组即异色
        dfs2(v, u);
    }
}

int main()
{
    int n;
    cin >> n;
    memset(head, -1, sizeof(head));
    for(int i = 1; i < n; i++)
    {
        int u, v;
        scanf("%d%d",&u,&v);
        add(u, v);
        add(v, u);
    }
    flag = true;
    dfs1(1, 0);
    if(flag == false || mrk[0] != 0)//后者是填色溢出
    {
        printf("-1");
        return 0;
    }
    dfs2(1, 0);
    for(int i = 1; i <= n; i++)
    {
        printf("%c",(col[i] == 0)?'R':'B');
    }
    return 0;
}

D 点一成零

bfs，并查集

思路

假设图中共有p组连通块，每一块包含cic_i格，则总方案数即为p!∗∏i=1pcip!*\prod_{i=1}^{p}c_i；

那么我们需要做的便是求出p与cic_i；

我们可以用遍历网格进行bfs创建并查集，并用并查集维护更改；

最开始抱有侥幸心理，我想对于每一次更改，遍历所有连通块以重新计算ans，结果爆了TLE；

对于具体的维护过程：
如果新增了一个面积为c的连通块，则ans=ans∗(p+1)∗cans=ans*(p+1)*c；
进一步地，如果一个面积为b的连通块，由于方块更新，并入了一个面积为a的连通块，则对这两个连通块来说（即不包括点的那个块，不过该块同理，面积为1）ans=ans/p/a/b∗(a+b)ans=ans/p/a/b*(a+b)；逆元处理除法即可；

使并查集的根为连通块中i∗n+ji*n+j最小的点

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll M=1e9+7,N=502;

pair<int ,int> fa[502][502];//father
map<pair<int,int>,int>cnt;//以[i][j]为根的并查集所代表的连通块的面积
queue<pair<int,int> >que;//bfs队列
int di[]={0,0,1,-1},dj[]={1,-1,0,0};
int mp[502][502],n,m,cou=0;

ll qm(ll a,ll b)//快速幂
{
    ll ans=1;
    for(;b;b>>=1)
    {if(b&1)ans=ans*a%M;
    a=a*a%M;}
    return ans;
}

pair<int,int> find(pair<int,int> pi)//并查集find
{
    if(fa[pi.first][pi.second]!=pi)fa[pi.first][pi.second]=find(fa[pi.first][pi.second]);
    return fa[pi.first][pi.second];
}

void bfs(pair<int,int> fat)
{
    int k;
    while(!que.empty())
    {
        pair<int,int>now=que.front();
        que.pop();
        for(k=0;k<4;k++)
        {
            int in=now.first+di[k],jn=now.second+dj[k];
            if(in>=0&&in<n&&jn>=0&&jn<n&&mp[in][jn]&&fa[in][jn]==make_pair(in,jn)&&!(in==fat.first&&jn==fat.second))
            {
                cnt[fat]++;
                fa[in][jn]=fat;
                que.push({in,jn});
                //printf("*%d\n",cnt[fat]);
            }
        }
    }
}

int main()
{
    int i,j,k;
    string g;
    cin>>n;
    for(i=0;i<n;i++)
    {
        cin>>g;
        for(j=0;j<n;j++)mp[i][j]=g[j]-'0',fa[i][j]={i,j};
    }
    //图接收完毕
    ll ans=1;
    for(i=0;i<n;i++)
        for(j=0;j<n;j++)
            if(mp[i][j]&&fa[i][j]==make_pair(i,j))
            {
                cou++;
                cnt[{i,j}]=1;
                que.push({i,j});
                bfs({i,j});
                ans*=(ll)cou*cnt[{i,j}];//计算初始ans
                ans%=M;
            }
    cin>>m;
    while(m--)
    {
        int ci,cj;
        scanf("%d%d",&ci,&cj);
        if(mp[ci][cj])printf("%lld\n",ans);//如果本来就是1，则图无任何变化
        else
        {
            mp[ci][cj]=1;//假定其为单独块
            cnt[{ci,cj}]=1;
            cou++;
            ans*=cou;
            ans%=M;//其作为单独块，更新ans，后面再修正
            pair<int,int> to={ci,cj};
            for(k=0;k<4;k++)//判断该及块四周的连通块形成的新连通块的根
            {
                int in=ci+di[k],jn=cj+dj[k];
                if(in>=0&&in<n&&jn>=0&&jn<n&&mp[in][jn])
                {
                    pair<int,int>fan=find({in,jn});
                    if(fan.first*n+fan.second<to.first*n+to.second)to=fan;
                }
            }
            if(make_pair(ci,cj)!=to)//如果新块的根不是自身，将自身并入新块根所在旧块
            {
                pair<int,int>fan=find({ci,cj});
                fa[fan.first][fan.second]=to;
                ans*=qm((ll)cou*(cnt[to]*cnt[fan])%M,M-2);
                cou--;
                ans%=M;
                cnt[to]+=cnt[fan];
                ans*=cnt[to];
                ans%=M;
            }
            for(k=0;k<4;k++)
            {
                int in=ci+di[k],jn=cj+dj[k];
                if(in>=0&&in<n&&jn>=0&&jn<n&&mp[in][jn])
                {
                    pair<int,int>fan=find({in,jn});
                    if(fan!=to)//把除新块根所在旧块以外的旧块并入新块根
                    {
                        fa[fan.first][fan.second]=to;
                        ans*=qm((ll)cou*(cnt[to]*cnt[fan])%M,M-2);
                        cou--;
                        ans%=M;
                        cnt[to]+=cnt[fan];
                        ans*=cnt[to];
                        ans%=M;
                    }
                }
            }
            printf("%lld\n",ans);
        }
    }
    return 0;
}

E 三棱锥之刻

立体几何

思路

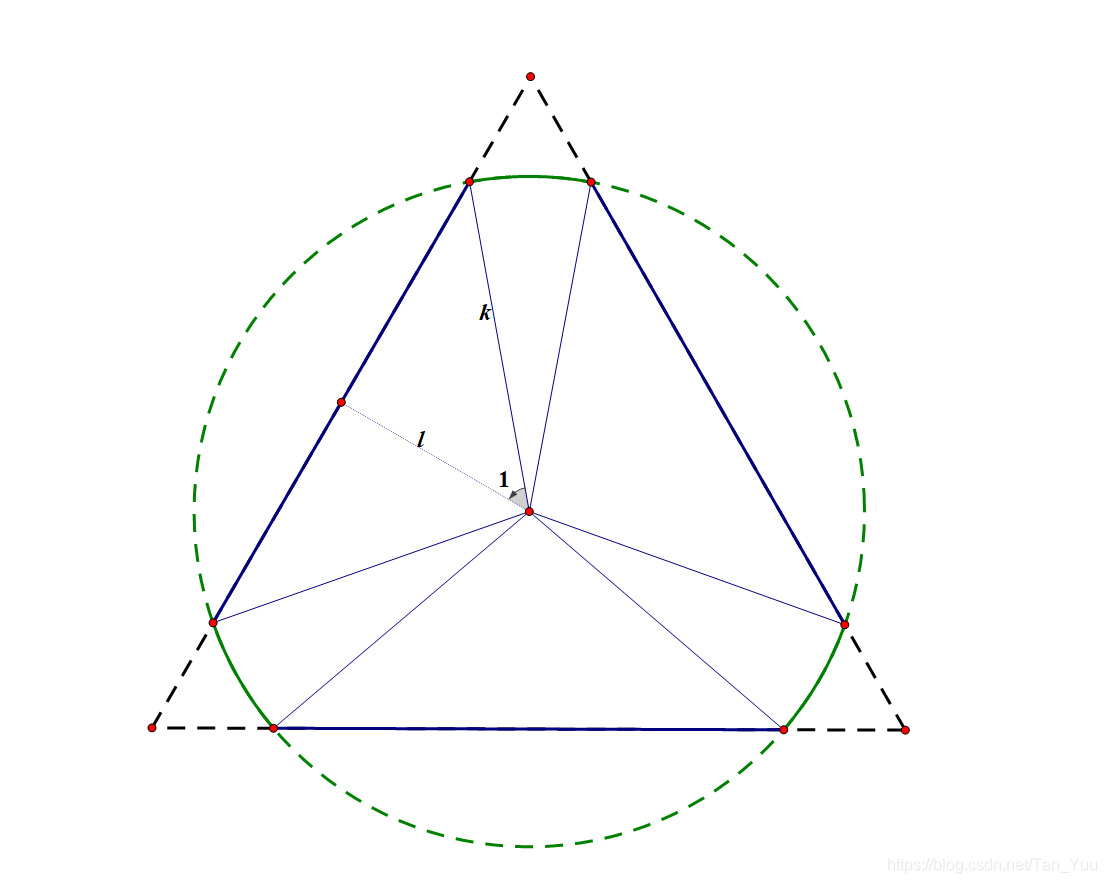
设中心点距面距离 ds ，距棱距离 da ，距顶点距离 dp ，喷漆半径 r
分为四种情况：

① r < ds
此种情况即无法喷到漆，面积为 0 ；

② ds <= r <= da
此种情况即每面被喷漆形状均为完整的圆，通过勾股定理求漆面半径，求圆面积即可；

③ da < r < dp
此种情况即为每面被喷漆形状为（三）弦切圆，如下图：
在这里插入图片描述

我将其分为三个三角形和一个扇形求面积，因为图中 k l 的长度均可求，便可使用 arccos 求出角度，进而得知扇形所占圆心角，进而求出扇形面积；

④ r >= dp
此时正四面体的四个面均被涂满，求三角形面积即可。

以下数据可参考，图源百度词条正四面体
在这里插入图片描述

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
#include <bits/stdc++.h>
using namespace std;
#define PI acos(-1)

int main()
{
    double r,a,d;
    cin>>a>>d;
    if(d*d-a*a/24<0) {printf("0");return 0;}//1
    r=sqrt(d*d-a*a/24);
    if(r<=a/2/sqrt(3))printf("%.5lf",4*PI*r*r);//2
    else if(r>a/2/sqrt(3)&&r<a/sqrt(3))//3
    {
        printf("%.5lf",(3*(sqrt(r*r-a*a/12)*a/2/sqrt(3))+PI*r*r*(2*PI-6*acos(a/2/sqrt(3)/r))/(2*PI))*4);
    }
    else printf("%.5lf",a*a*sqrt(3));//4
    return 0;
}

F 对答案一时爽

贪心

思路

最小值当然是 0 ，最大值即为两人答题总数 - 答案相异数。

假设一人全对，此时即为最大值。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
#include <bits/stdc++.h>
using namespace std;

int main()
{
    int n,sa=0,i,c=0;
    char a[202],b[202],g;
    cin>>n;
    getchar();
    c=0;
    while(c!=n)
    {
        g=getchar();
        if(g>='A'&&g<='Z')
        a[c++]=g;
    }
    getchar();
    c=0;
    while(c!=n)
    {
        g=getchar();
        if(g>='A'&&g<='Z')
        b[c++]=g;
    }
    for(i=0; i<n;i++)

            if(a[i]==b[i])sa++;

    printf("%d %d",sa+n,0);
    return 0;
}

字符串处理一团糟…

H 幂塔个位数的计算

找规律

思路

具体推倒过程过于繁琐，主要是通过a%10a\%10的结果推倒aa%10a^{a}\%10的结果，再进行迭代。
结果会在大概三层之内收束到定值。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
char a[100005],n[100005];
int main()
{
	scanf("%s%s",a,n);
	ll la=strlen(a),ln=strlen(n);
	if(ln==1 && n[0]=='1')
	{
		printf("%d\n",a[la-1]-'0');
		return 0;
	}
	else
	{
		int a1=a[la-1]-'0';
		int b=((a[la-2]-'0')*10+a[la-1]-'0')%4;
		if(a1==0 || a1==1 || a1==5 || a1==6 || a1==9)
		{
			printf("%d\n",a1);
		}
		else if(a1==4)
		{
			printf("6\n");
		}
		else if(a1==2 || a1==8)
		{
			if(ln==1 && n[0]=='2' && b!=0)
			{
				printf("4\n");
			}
			else
			{
				printf("6\n");
			}
		}
		else if(a1==3)
		{
			if(b==1)
			{
				printf("3\n");
			}
			else
			{
				printf("7\n");
			}
		}
		else if(a1==7)
		{
			if(b==1)
			{
				printf("7\n");
			}
			else if(b==3)
			{
				printf("3\n");
			}
		}
		return 0;
	}
}

I 限制不互素对的排列

构造

思路

要用 [ 1 , n ] 的 n 个数构造出含 k ( k <= n / 2 ) 对非互质数对的数列，首先我们想到的就是用偶数构造所求部分，然后顺序排列其他数。

接下来除法默认向下取整

具体来说，对于某偶数 2 * i ，一定与 2 * ( i + 1 ) 不互质；对于某奇数 2 * i + 1 ，一定与 2 * ( i + 1 ) + 1 互质；对于 >= 2 的正整数 i ，一定与 i + 1 互质。

依照以上三条性质，如果输入值为 8 3 我们便可以构造出 [ 2 , 4 , 6 , 8 , 1 , 3 , 5 , 7 ] 与此同时，便发现了一个问题：对于前 n 个数，含有 ⌊ n / 2 ⌋ 个偶数，最多构成 ⌊ n / 2 ⌋ - 1 个偶数对，但是 k <= n / 2 。

解决此种问题，我们可以进一步处理，选择满足以下性质的某偶数：可以表示为 2 * ( 2 * i + 1 ) ，即可以拆成 2 和某奇数的积。将此偶数放在偶数部分末尾，后再接该奇数，则可保证有 k 对非互质数对。

对于该偶数，10,14,18,…,34,…,122,… 均满足条件，但是满足条件的最小数是 6 。取最小数除了方便处理之外，同时也方便可行判定。

此时，本题的输入便有三种情况：

① n < 6 && k = n / 2
此时无可行解，输出 -1；

② n > 6 && k < n / 2
此时输出前 k + 1 个偶数后，其余数依次输出即可；

③ n > 6 && k = n / 2
此时输出除 6 外的前 k - 1 个偶数后，输出 6 3 ，再依次输出其余数。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
#include <bits/stdc++.h>
using namespace std;

int main()
{
    int n,k,i;
    cin>>n>>k;
    if(n<6&&k==n/2)printf("-1");//1
    else if(k==n/2)//3
    {
        for(i=1;i<=n/2;i++)if(i!=3)printf("%d ",2*i);
        printf("6 3 1 ");
        for(i=5;i<=n;i+=2)printf("%d ",i);
    }
    else//2
    {
        for(i=1;i<=k+1;i++)printf("%d ",2*i);
        for(i=1;i<=n;i++){if(i%2==0&&i/2<=k+1)continue;printf("%d ",i);}
    }
    return 0;
}

J 一群小青蛙呱蹦呱蹦呱

思路

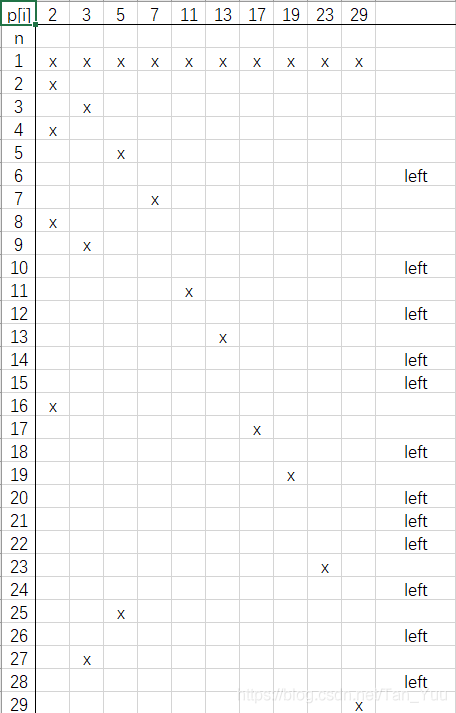
我们手动模拟可知，剩下的数是质因子个数大于等于二的数，也就是说，剩下的数均可表示为 p1^m1 * p2^m2 * … * pn^mn ( n >= 2 )。如下图
在这里插入图片描述
对于范围内的所有质数 p[ i ] ，第 j 个剩下的数可以表示为 p1^m1j * p2^m2j * … * pn^mnj 则所有剩下的数的最小公倍数则为 p1^max( m11 , m12 , m13, … , m1j ) * p2^max( m21 , m22 , m23, … , m2j ) * … * pn^max( mn1 , mn2 , mn3, … , mnj) 。
接下来我们的任务就是求出 max() 。

对于 >= 2 的任意 p[ i ] ，小于 N （范围）且 含有 p[ i ] 幂次最大的 剩余数显然是 2 * p[ i ]^m ，则可以求出 m = logp[i]n/2；

对于质数 2 ，最大数则是 3 * 2m ,此时 m = log2n/3 。

之后累乘 p[ i ]m 即可。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
#include <bits/stdc++.h>
using namespace std;
const long long MOD = 1e9 + 7;
const long long N=80000007;
long long qs(long long a,long long t)//快速幂取模
{
    long long ans=1;
    while(t)
    {
        if(t&1)ans=ans*a%MOD;
        a=a*a%MOD;
        t>>=1;
    }
    return ans%MOD;
}
static int p[N];
static bool n[N];

int main()
{
    n[0]=1,n[1]=1;
    int i,j,c=0;
    for(i=2;i<=N;i++)//线性筛
    {
        if(!n[i])p[c++]=i;
        for(j=0;j<c&&i*p[j]<=N;j++)
        {
            n[i*p[j]]=1;
            if(i%p[j]==0)break;
        }
    }
    int n;//与前面的数组名重复了，但是编译运行没有问题，可能不太好理解
    cin>>n;
    if(n<6){printf("empty");return 0;}
    long long ans=qs(2,(long long)log2(n/3.0));//对2
    for(i=1;p[i]<=n/2&&i<c;i++)//对其他
    {
        ans%=MOD;
        ans*=qs(p[i],(long long)(log2(n/2.0)/log2(p[i]*1.0)));//浮点除法&换底公式
    }
    printf("%lld",ans%MOD);
    return 0;
}

附：关于线性筛的优化，可以参照这里，（代码未体现）

ED

《 基 础 选 手 》

算法竞赛 > 比赛与题集
2021牛客寒假算法基础集训营1（A B C D E F H I J）
https://tanyuu.github.io/2021.01-06/2021牛客寒假算法基础集训营1（A B C D E F H I J）/
作者
F Juny
发布于
2021年2月3日
许可协议