四点共圆的判定

题目来源：NEFU OJ-2248&
湖南大学2020届ACM新生赛(同步赛) F

OP

此题不难，只不过推导比较闹心，多推几遍就AC了。

思路

判断四点共圆，特殊方法是对角互补，但是由于此题中未强调顺序，判断对角有一定的难度。故采用更通用的方法：

设四点为A，B，C，D（顺序无关）
先任取三点A、B、C
当A、B、C 不共线时：

\首先通过AB、AC的中垂线交点确定距此三点距离相等的点，并假定其为圆心；
\再计算半径，并与第四点到假定圆心的距离进行比较，从而判断第四点是否共圆。

当A、B、C 共线时：

\显然没有圆满足与一条直线有三个交点，故四点不共圆。

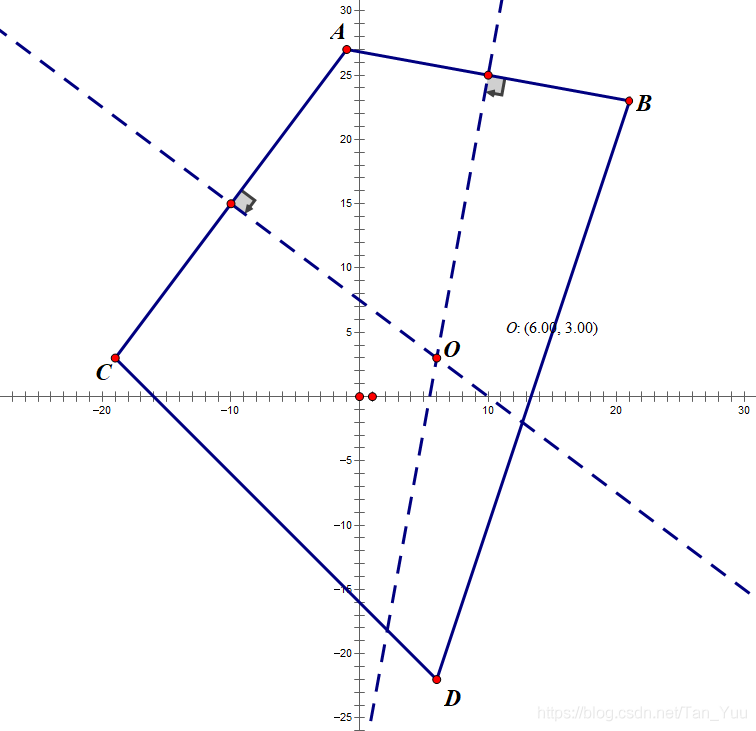
具体实现上，可以通过中学的平面几何知识构造中垂线方程，解假定圆心，只不过推导较为繁琐。

代码

#include <bits/stdc++.h>
using namespace std;

int main()
{
    double x[4],y[4],xo,yo,down;
    int t,i,j;
    cin>>t;
    while(t--)
    {
        for(i=0; i<4; i++)cin>>x[i]>>y[i];
        down=(x[2]-x[0])*(y[0]-y[1])-(x[1]-x[0])*(y[0]-y[2]);
        down*=-1;
        if(fabs(down)<=1e-10)printf("no\n");//判断三点共线
        else
        {
            xo=(x[0]*x[0]-x[2]*x[2])*(y[0]-y[1])/2-(x[0]*x[0]-x[1]*x[1])*(y[0]-y[2])/2+(y[0]-y[2])*(y[0]-y[1])*(y[2]-y[1])/2;
            xo/=down;
            yo=(x[1]-x[0])/2*(-(x[0]*x[0]-x[2]*x[2])-(y[0]*y[0]-y[2]*y[2]))-(x[2]-x[0])/2*(-(x[0]*x[0]-x[1]*x[1])-(y[0]*y[0]-y[1]*y[1]));
            yo/=down;
            yo*=-1;
            //printf("%lf %lf\n",xo,yo);
            if(fabs((x[0]-xo)*(x[0]-xo)+(y[0]-yo)*(y[0]-yo)-(x[3]-xo)*(x[3]-xo)-(y[3]-yo)*(y[3]-yo))<=1e-10)
                 printf("yes\n");
            else printf("no\n");
        }
    }
    return 0;
}

ED

此种方法也可以拓展为判断n点共圆；

推 导 时 注 意 正 负 号 ！