关于 阿华分硬币 一题的思路+注意点+代码（数组分成差最小的两部分）

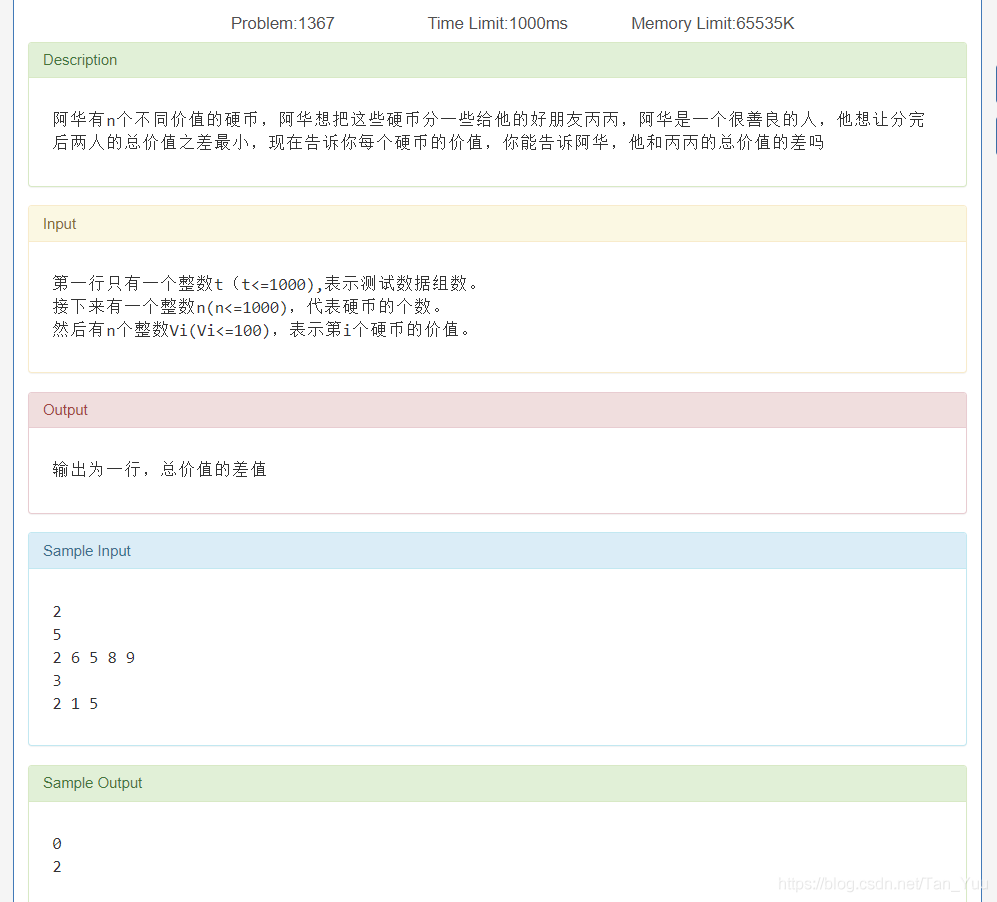
题目来源：NEFU OJ-1367 阿华分硬币

OP

DP

思路

首先这个数据量，穷举遍历是行不通的，所以计划用dp，类似于0-1背包问题

对于这个题我们可以如下构造：b[i][j]为在有前 i 枚硬币时，选出不超过 j 的最大金额值。(不需要担心大于or小于总金额一半到问题，因为若能组成大于总金额一半且差值最小的组合，则另一半即为小于总金额一半且差值最小的组合)

接下来的a[i]代表第i枚硬币的面值

那么状态转换就是 b[i][j] = max ( b[i-1][j] , b[i-1][j-a[i]] + a[i] )
语言表述就是 有前i每硬币时，选出不超过j的最大总额是 在没有第i枚硬币时，不超过j的总额最大值 与 在没有第i枚硬币时，不超过j-a[i]的总额最大值加上a[i] 的最大值。

到此时，这道题理论上（我没试）就可以AC了。

向一维化简及注意事项

这道题与NEFU OJ-971 硬币数目（之前的文章）&NEFU OJ-1717 货币系统不同的是，这道题的每一枚硬币都只能用一次。
换句话说，对于一维的状态转换方程————b[j] = max ( b[j] , b[j-a[i]] + a[i] )，b[j-a[i]]这一项必须是维护前的。为解决这个问题，不同于前提两题，j我打算从后向前维护，这样就不会出现同一枚硬币被计算多次的情况。

以样例二为例，如果从前向后维护，则会出现如下情况：

a[i]\b[j]	0	1	2	3	4
0	0	0	0	0	0
2	0	0	2	2	4
……

此时，b[1][4]=4 , 即用了两次二面值硬币，显然是有违题意的。
从后向前则为

a[i]\b[j]	0	1	2	3	4
0	0	0	0	0	0
2	0	0	2	2	2
1	0	1	2	3	3
5	0	1	2	3	3

5本身就已经大于(最大值 / 2 )了，所以不需要处理，落下来即可。

代码

#include <bits/stdc++.h>
using namespace std;

int main()
{
    int t,i,j;
    cin>>t;
    while(t--)
    {
        int n,a[1003],l,r,del,sum=0,b[50004]={0};
        scanf("%d",&n);
        for(i=1;i<=n;i++){scanf("%d",&a[i]);sum+=a[i];}
        for(i=1;i<=n;i++)
        {
            for(j=sum/2;j>=a[i];j--)//从sum/2开始就够，不需要关心上下取整
            {
                b[j]=max(b[j],b[j-a[i]]+a[i]);
            }
        }
        printf("%d\n",(int)(2*(sum/2.0-b[sum/2])));//注意保留浮点
    }
    return 0;
}

ED

\