关于 网络延时 一题的思路+代码（树的后序遍历&DP）

题目来源：Acwing-3215.网络延时

题目描述

给定一个公司的网络，由 n 台交换机和 m 台终端电脑组成，交换机与交换机、交换机与电脑之间使用网络连接。
交换机按层级设置，编号为 1 的交换机为根交换机，层级为 1。
其他的交换机都连接到一台比自己上一层的交换机上，其层级为对应交换机的层级加 1。
所有的终端电脑都直接连接到交换机上。
当信息在电脑、交换机之间传递时，每一步只能通过自己传递到自己所连接的另一台电脑或交换机。
请问，电脑与电脑之间传递消息、或者电脑与交换机之间传递消息、或者交换机与交换机之间传递消息最多需要多少步。

输入描述

输入的第一行包含两个整数 n,m，分别表示交换机的台数和终端电脑的台数。
第二行包含 n−1 个整数，分别表示第 2、3、……、n 台交换机所连接的比自己上一层的交换机的编号。第 i 台交换机所连接的上一层的交换机编号一定比自己的编号小。
第三行包含 m 个整数，分别表示第 1、2、……、m 台终端电脑所连接的交换机的编号。

输出描述

输出一个整数，表示消息传递最多需要的步数。

数据范围

前 30% 的评测用例满足：n≤5,m≤5。
前 50% 的评测用例满足：n≤20,m≤20。
前 70% 的评测用例满足：n≤100,m≤100。
所有评测用例都满足：1≤n≤10000，1≤m≤10000。

输入样例1

4 2
1 1 3
2 1

输出样例1

4

输入样例2

4 2
1 1 3
2 1

输出样例2

4

输入样例3

15 10
1 7 1 2 2 1 1 4 2 1 1 11 13 2
11 3 8 9 13 10 6 12 7 12

输出样例3

6

OP

样例3是测试组之一，反映了一些前两个样例没有的情况，下面会具体解释。

思路

首先对于这道题，交换机与电脑几乎没有区别，只是电脑一定作为末端，所以在处理时不需要特殊区分。

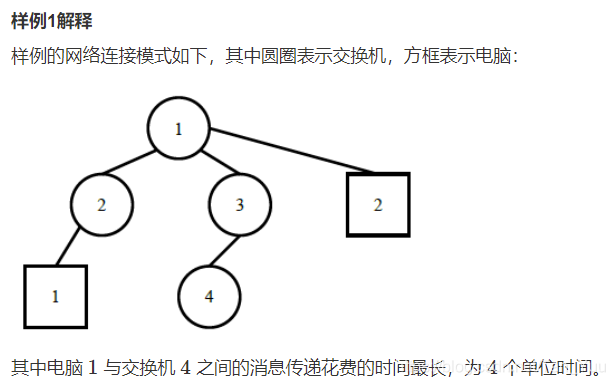
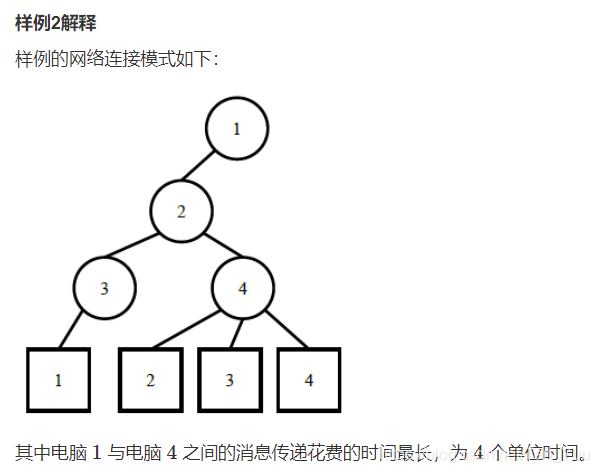
对于题求的消息传递最多需要的步数，可以分为两大种情况，一种是如样例1、2图示，最长距离两点在同一节点下不同的子树，另一种情况是两点存在亲子关系，即一个点在以另一点为根的子树的叶节点上。

对于第二种情况，消息传递最多需要的步数显然是根节点（1号交换机）与深度最大的叶节点（电脑或交换机）构成的对。

第一种情况，我们可以做如下处理：

对于最小值的情况，我们可以看成是该节点下 不同子树的 两个深度最深的 叶子的 深度之和。

我们可以后序遍历该树，对于每一个节点的深度先初始化为0。对于节点 i ，其父节点 fa[ i ] 的深度 dpl[ fa[ i ] ] = max( dpl[ fa[ i ] ] , dpl[ i ]+1 ) ，这样我们便可以得到每一个点的所在深度（到以其为根的子树的最远叶节点的距离）。

再对于所有度>=2 的节点，找到 dpl 最大的两个叶节点，则以该点（度>=2的点）为根的子树的题求量则为 dpl_max1 + dpl_max2 + 2 ，再更新目前题求量的最大值即可。

在构建后序遍历时，不能直接通过序号降序遍历，如样例三，则会出现一些问题：7在3之前被遍历，而后序遍历则是3在7前。

代码

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
int dpl[20004],fa[20004]={0,0};//fa存上级节点
vector<int>son[20004];//存下级节点
stack<int>order;
void eno(int x)//构建后序遍历栈
{
    order.push(x);
    int i;
    for(i=0;i<son[x].size();i++)
    {
        eno(son[x][i]);
    }
}
int main()
{
    memset(dpl,0,sizeof dpl);
    int n,m,i,j,g,ans=0;
    cin>>n>>m;
    for(i=2;i<=n;i++)//接收交换机
    {
        scanf("%d",&g);
        fa[i]=g;
        son[g].push_back(i);
    }
    for(;i<=n+m;i++)//接收电脑
    {
        scanf("%d",&g);
        fa[i]=g;
        son[g].push_back(i);
    }
    eno(1);
    while(order.size())
    {
        i=order.top();
        order.pop();
        dpl[fa[i]]=max(dpl[fa[i]],dpl[i]+1);//更新上级节点的dpl
        if(son[i].size()>=2)//度>=2
        {
            int mx1=0,mx2=0;
            for(j=0;j<son[i].size();j++)//找最大的两个叶节点dpl
            {
                if(dpl[son[i][j]]>mx1)
                {
                    mx2=mx1;
                    mx1=dpl[son[i][j]];
                }
                else if(dpl[son[i][j]]==mx1||dpl[son[i][j]]>mx2)
                {
                    mx2=dpl[son[i][j]];
                }
            }
            ans=max(ans,mx1+mx2+2);//更新题求量
        }
    }
    ans=max(ans,dpl[1]);//与第二大类情况做比较
    cout<<ans;
    return 0;
}

ED

\