关于 硬币购物 一题的思路+难点分析+代码 (DP + 容斥)
题目来源:/*这个题好经典的,哪里都有*/ NEFU OJ-1793 硬币购物-容斥
题目描述
硬币购物一共有4种硬币。面值分别为c1,c2,c3,c4。某人去商店买东西,去了tot次。每次带di枚ci硬币,买si的价值的东西。请问每次有多少种付款方法。
输入描述
第一行 c1,c2,c3,c4,tot 下面tot行 d1,d2,d3,d4,s
输出描述
每次的方法数
输入样例
1 2 5 10 2
3 2 3 1 10
1000 2 2 2 900输出样例
4
27提示
数据规模
di,s<=100000
tot<=1000
OP
这道题我也是研读了好多位其他博主的文章而通过的,感谢各位前辈。
直接来说,我认为这道题对我的难点有二:容斥的构造和对dp过程数据的处理
思路
首先排除DFS,这个数据量一定TLE。
这道题中,相同面值硬币的不同枚之间是完全相同的,所以就无法对所有枚硬币进行背包。
我们只好先不关注四种硬币的数量限制,进行dp,之后再用容斥处理不合法的组合。
难点分析
容斥的构建
如果不了解容斥,可以向下看
对于不合法的种类,我们可以有交集地分为四类:第一种硬币数量不合法、第二种硬币不合法、第三种…、第四种…。(这样方便用代码实现)
这四类之间相互有交集,我们如果想计算不合法的总种类数,就需要妥善处理交集。
以三种硬币为例:(四种同理,三种表示起来更直观)
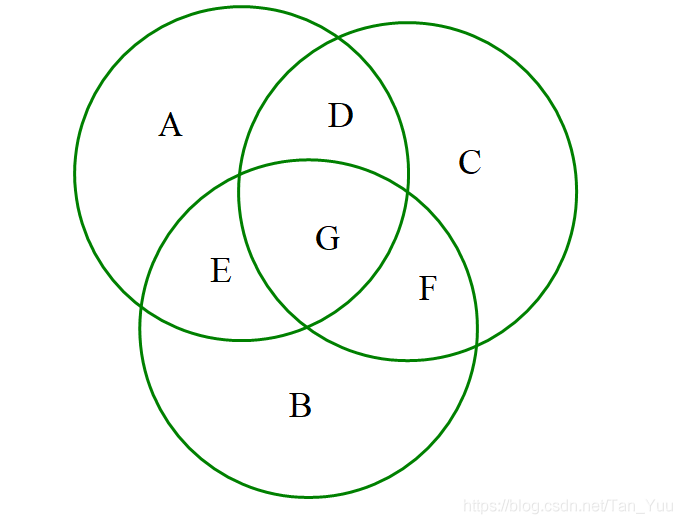
我们暂时称左上圆(A,D,G,E)为O1,右上圆(C,D,G,F)为O2,下圆为O3。
如果我们要求这个最大封闭图形的面积,可以通过O1+O2+O3-(O1∩O2)-(O1∩O3)-(O2∩O3)+(O1∩O2∩O3)来实现
数学上更广泛来说就是
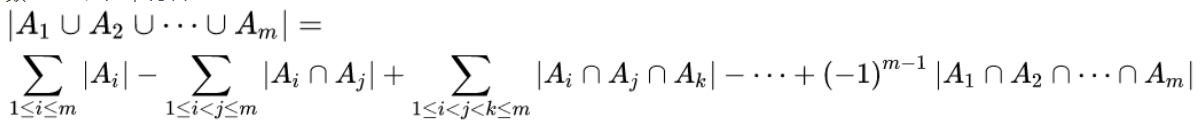
(图源百度)(如果还是不太理解可以移步这里)
对dp过程数据的处理
所以此时,我们此题的答案即为 无限制的种类数 - 存在1种硬币非法的种类数(4项) + 存在2种硬币非法的种类数(6项) - 存在3种硬币非法的种类数(4项) + 4种硬币均非法的种类数(1项)。
接下来我们要找出不同情况的种类数。
目标金额 s 时,对于第 i 枚硬币,面值为 c[ i ],数量为 d[ i ],如果存在 s >= ( d[ i ] + 1 ) * c[ i ],则一定该种硬币存在非法情况。同理,对于第 i , j 枚硬币,如果存在 s >= ( d[ i ] + 1 ) * c[ i ] + ( d[ j ] + 1 ) * c[ j ],则这两种硬币一定同时存在非法情况。
那么对于具体的非法种类数即为:f[ s - ( d[ i ] + 1 ) * c[ i ] ],因为 f[ s ] 是建立于 f[ s - ( d[ i ] + 1 ) * c[ i ] ] 之上的,所以说作差之后,便可认为成 从 s - ( d[ i ] + 1 ) * c[ i ] + 1 到 s 的所有方法数,此时,每一种情况的第 i 种硬币枚数必不超过 d[ i ] 。
也就是说, f[ s - ( d[ i ] + 1 ) * c[ i ] ] 中的每一种情况延伸到 f[ s ] 时,必有一种分支情况存在,满足第 i 种硬币的数量为 d[ i ] + 1(存在性),同时,绝对没有任一种情况满足第 i 种硬币的数量大于 d[ i ] + 1(因为那样总金额必然大于 s )(唯一性),在 f[ s - ( d[ i ] + 1 ) * c[ i ] ] 中的每种情况的非法延申存在且唯一,所以删去的便是全部的非法情况。
同理,多个硬币同时非法时,f[ s - ( d[ i ] + 1 ) * c[ i ] - ( d[ j ] + 1 ) * c[ j ] ] 即可。
附
最后附一张第一样例的二维dp表,方便大家验算

代码
1 | |
ED
感觉证明非法延申存在且唯一的部分可能会比较难懂,但是个人认为很重要,题解第一稿中直接略过了证明,感觉很不妥便加回来了,如有疏漏或逻辑问题,烦请提醒。