关于 牛异或 一题的思路+代码（01字典树的构建与查询）

题目来源：Acwing 1414.牛异或（usaco training 6.1）

题目描述

农夫约翰在给他的奶牛们喂食时遇到了一个问题。
他共有 N 头奶牛，编号 1∼N。
每次喂食前，这 N 头奶牛会按照 1∼N 的顺序站成一排。
此外，每头奶牛都被分配了一个可能不唯一的整数。
那么所有被分配的整数就形成了一个长度为 N 的整数序列。
请你在该整数序列中找出一个连续的非空子序列，使得子序列中元素的异或和能够最大。
如果存在多个这样的序列，那么选择序列末端整数对应的奶牛编号更小的那个序列。
如果仍然存在多个可选的序列，那么选择长度最短的那个序列。

输入描述

第一行包含整数 N。
第 2∼N+1 行，每行包含一个整数，其中第 i 行的整数表示编号为 i−1 的牛被分配的整数值。

输出描述

输出三个整数，分别表示最大的异或和，所选序列首端整数对应的奶牛编号，所选序列末端整数对应的奶牛编号。

数据范围

1≤N≤10⁵ ，
分配给奶牛的整数的范围是 [0,2²¹−1]。

输入样例1

5
1
0
5
4
2

输出样例1

6 4 5

OP

关于字典树，网上的介绍已经很详细了（可以参照这里），我在这里补充一点，也是自己遇到过的困难：
对于具体的存储过程，实际上是将树状结构通过“路标”存储为线性结构；

（图源上链）

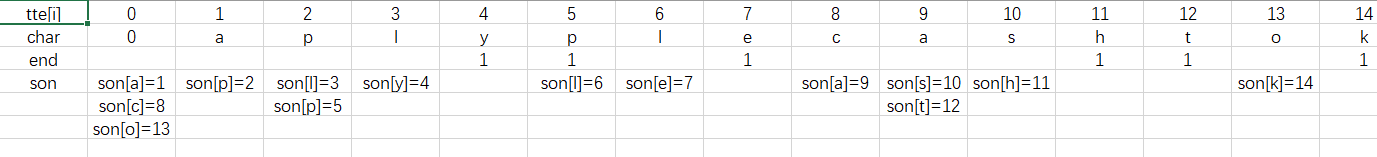
思路

由于异或运算有着 a^b^a=b 的性质，所以我们可以使用类似于前缀和的结构快速获取连续区间的异或值。

如果对于每一个右端点遍历左端点，时间复杂度即为 O(n²)，会TLE；

所以我们需要使用01字典树存储前面 i 个前缀，将每一个新的前缀作为右端点，搜索异或值最大的左端点，并更新答案，时间复杂度为 O(nlog2(21))；

值得提出的是，在这道题中，每一个节点代表的具体值不需要在其节点内部特殊记录。由于指向每一个节点的节点有且只有一个，该节点的值即为指向其的“路标”对应的值。

代码

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;

int idx=0;//记录节点开到了哪里
struct trietree
{
    int son[2]={0,0};
    int end=-1;
}tte[800005];//节点数组
void btre(int x,int ni)
{
    int i,index=0;
    for(i=21;i>=0;i--)
    {
        int n=(x>>i)&(1);
        if(tte[index].son[n])//如果此枝被定义过
        {
            index=tte[index].son[n];//顺至此枝
        }
        else//如果此枝未被定义
        {
            tte[index].son[n]=++idx;//定义
            index=tte[index].son[n];//顺至此枝
        }
        if(!i)tte[index].end=ni;//给末尾覆盖标记
    }
}
pair<int,int> checktree(int x)
{
    int i,ans=0,index=0,end=-1;
    for(i=21;i>=0;i--)
    {
        int n=(x>>i)&(1);
        if(tte[index].son[!n])//如果反向枝被定义过
        {
            ans+=(1<<i);//printf("1");//异或值更新
            index=tte[index].son[!n];//顺至反向枝
        }
        else index=tte[index].son[n];//printf("0");//如果反向枝没被定义过，异或值当为即为0，不需要特殊更新，顺至同向枝
    }
    end=tte[index].end;//获取对应编号
    return {ans,end};//返回{异或值，起始编号}
}
int main()
{
    int n,i,six=0,g;//a[100005]={0};
    cin>>n;
    btre(six,0);//对前缀0建树
    int bgn=1,end=1,ans=0;
    for(i=1;i<=n;i++)
    {
        scanf("%d",&g);
        six^=g;//获取异或前缀值
        pair<int,int> z=checktree(six);
        btre(six,i);//更新树
        if(z.first>ans)
        {
            ans=z.first,bgn=z.second+1,end=i;//更新
        }
    }
    printf("%d %d %d",ans,bgn,end);
    return 0;
}

ED

字典树需要注意的细节蛮多的