关于 压缩编码 一题的思路+解法（区间DP）

题目来源：Acwing.3240 压缩编码

题目描述

给定一段文字，已知单词 a1,a2,…,an 出现的频率分别 t1,t2,…,tn。
可以用 01 串给这些单词编码，即将每个单词与一个 01 串对应，使得任何一个单词的编码（对应的 01 串）不是另一个单词编码的前缀，这种编码称为前缀码。
使用前缀码编码一段文字是指将这段文字中的每个单词依次对应到其编码。
一段文字经过前缀编码后的长度为：
L=a1 的编码长度 ×t1+a2 的编码长度 ×t2+…+an 的编码长度 ×tn。
定义一个前缀编码为字典序编码，指对于 1≤i<n，ai 的编码（对应的 01 串）的字典序在 ai+1 编码之前，即 a1,a2,…,an 的编码是按字典序升序排列的。
例如，文字 E A E C D E B C C E C B D B E 中， 5 个单词 A、B、C、D、E 出现的频率分别为 1,3,4,2,5，则一种可行的编码方案是 A:000, B:001, C:01, D:10, E:11，对应的编码后的 01 串为 1100011011011001010111010011000111，对应的长度 L 为 3×1+3×3+2×4+2×2+2×5=34。
在这个例子中，如果使用哈夫曼(Huffman)编码，对应的编码方案是 A:000, B:01, C:10, D:001, E:11，虽然最终文字编码后的总长度只有 33，但是这个编码不满足字典序编码的性质，比如 C 的编码的字典序不在 D 的编码之前。
在这个例子中，有些人可能会想的另一个字典序编码是 A:000, B:001, C:010, D:011, E:1，编码后的文字长度为 35。
请找出一个字典序编码，使得文字经过编码后的长度 L 最小。
在输出时，你只需要输出最小的长度 L，而不需要输出具体的方案。
在上面的例子中，最小的长度 L 为 34。

输入描述

输入的第一行包含一个整数 n，表示单词的数量。
第二行包含 n 个整数，用空格分隔，分别表示 a1,a2,…,an 出现的频率，即 t1,t2,…,tn。
请注意 a1,a2,…,an 具体是什么单词并不影响本题的解，所以没有输入 a1,a2,…,an。

输出描述

输出一个整数，表示文字经过编码后的长度 L 的最小值。

数据范围

对于 30% 的评测用例，1<n≤10，1≤ti≤20；
对于 60% 的评测用例，1<n≤100，1≤ti≤100；
对于 100% 的评测用例，1<n≤1000，1≤ti≤10000。

输入样例1

5
1 3 4 2 5

输出样例1

34

时空限制

3s / 256MB

OP

参考了大佬的题解；
关于哈夫曼树可以参考这里。

思路

若使用哈夫曼树，则

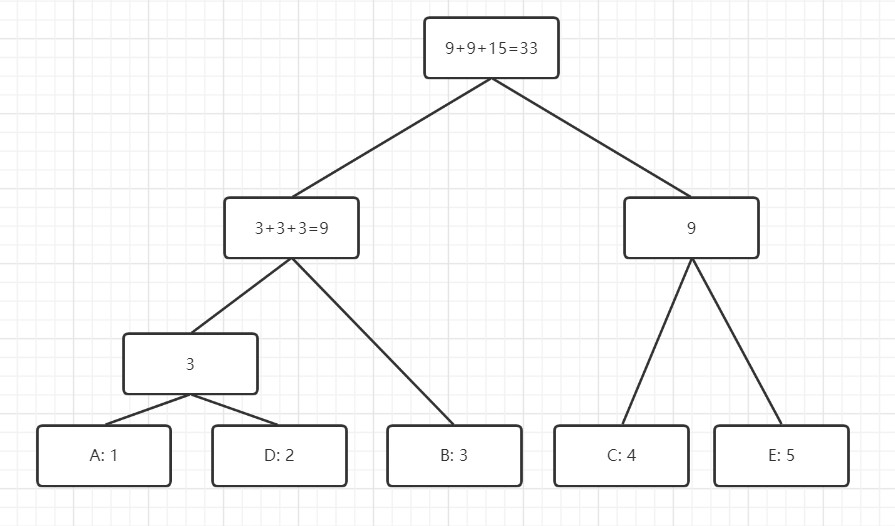
（图源题解链）
若使用字典序升序编码，则

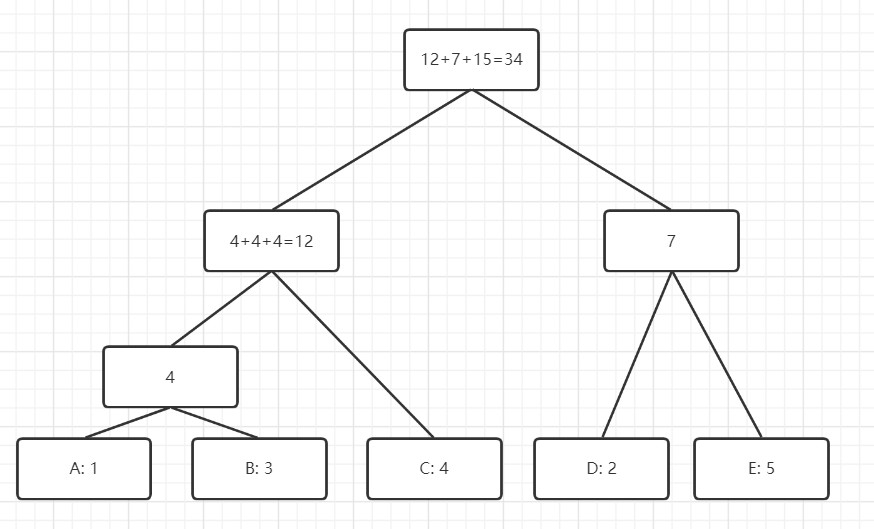
（图源题解链）
前者每次合并代价最小的两节点，而后者由于字典序的要求，每次只能合并相邻且代价最小的两节点。

这样我们便可以使用区间DP来求解最小值；

每次合并，合并后编、码总长度即增加了合并量；

建立区间dp方程：

$dp[l][r]=min(dp[l][k]+dp[k+1][r]+\sum_{i=l}^ra[i]),(k\in[l,r])$

对于求和项，我们可以用前缀和来解决；

时间复杂度$O(n^3)$，时间限制3s，所以问题不大。

代码

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;

int main()
{
	int n,i,j,a[1003],root=0,dp[1003][1003];
	stack<int>ls;
	cin>>n;
	for(i=1;i<=n;i++)scanf("%d",&a[i]),a[i]+=a[i-1];//接收，构建前缀和
	for (int len = 2; len <= n; ++len)//遍历区间长
        for (int l = 1; l + len - 1 <= n; ++l)//遍历左端点
		{
            int r = l + len - 1;//计算右端点
            dp[l][r] = 1e8;//初始化
            for (int k = l; k <= r; ++k)//遍历断点
			{
                dp[l][r] = min(dp[l][r], dp[l][k] + dp[k + 1][r] + a[r] - a[l - 1]);//更新min
            }
    	}
	cout<<dp[1][n];
    return 0;
}

ED

\